算法的实际应用
Bitmap 的巧用
关于用户标签的需求
实现用户信息的标签化。用户标签包括用户的社会属性、生活习惯、消费行为等信息。通过用户标签,可以对多样的用户群体进行统计。例如:统计用户的男女比例、统计喜欢旅游的用户数量等。
为了满足用户标签的统计需求,利用关系数据库设计了如下的表结构,每一个维度的标签对应着数据库表中的一列:
| Name | Sex | Age | Occupation | Phone |
|---|---|---|---|---|
| 张三 | 男 | 90后 | 程序员 | 苹果 |
| 李四 | 男 | 90后 | 程序员 | 三星 |
| 王五 | 女 | 00后 | 学生 | 小米 |
要想统计所有 “90后” 的程序员,用一条求交集的 SQL 语句即可。
Select count (distinct Name) as 用户数 from table where Age="90后" and Occupation="程序员";
要想统计所有使用苹果手机或 “00后” 的用户总和,用一条求并集的 SQL 语句即可。
Select count (distinct Name) as 用户数 from table where Phone="苹果" or Age="00后";
之后标签越来越多,筛选的标签条件过多的时候,拼出来的 SQL 语句像面条一样长……不仅如此,当对多个用户群体求 并集 时,需要用 distinct 来去掉重复数据,性能实在太差了……
解决方法
Bitmap 算法,中文里叫作 位图算法。是内存中连续的二进制位(bit)所组成的数据结构,该算法主要用于对大量整数做去重和查询操作。
假设给出一块长度为 10bit 的内存空间,也就是 Bitmap,想要依次插入整数 4、2、1、3,具体步骤如下:
第一步,给出一块长度为 10 的 Bitmap,其中的每一个 bit 位分别对应着从 0 到 9 的整型数。此时,Bitmap 的所有位都是 0。
num: 0 0 0 0 0 0 0 0 0 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
第二步,把整型数 4 存入 Bitmap,对应存储的位置就是下标为 4 的位置,将此 bit设置为 1。
num: 0 0 0 0 0 1 0 0 0 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
第三步,把整型数 2 存入 Bitmap,对应存储的位置就是下标为 2 的位置,将此 bit设置为 1。
num: 0 0 0 0 0 1 0 1 0 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
第四步,把整型数 1 存入 Bitmap,对应存储的位置就是下标为 1 的位置,将此 bit设置为 1。
num: 0 0 0 0 0 1 0 1 1 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
第五步,把整型数 3 存入 Bitmap,对应存储的位置就是下标为 3 的位置,将此 bit设置为 1。
num: 0 0 0 0 0 1 1 1 1 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
Bitmap 不仅方便查询,还可以去掉重复的整数。让每一个标签存储包含此标签的所有用户 ID。
| Name | Sex | Age | Occupation | Phone |
|---|---|---|---|---|
| 张三 | 男 | 90后 | 程序员 | 苹果 |
| 李四 | 男 | 90后 | 程序员 | 三星 |
| 王五 | 女 | 00后 | 学生 | 小米 |
第一步,建立用户名和用户ID 的映射。
| ID | Name |
|---|---|
| 1 | 张三 |
| 2 | 李四 |
| 3 | 王五 |
第二步,让每一个标签存储包含此标签的所有用户 ID,每一个标签都是一个独立的 Bitmap。
| Sex | Bitmap |
|---|---|
| 男 | 1, 2 |
| 女 | 3 |
| Age | Bitmap |
|---|---|
| 90后 | 1, 2 |
| 00后 | 3 |
| Occupaton | Bitmap |
|---|---|
| 程序员 | 1, 2 |
| 学生 | 3 |
| Phone | Bitmap |
|---|---|
| 苹果 | 1 |
| 三星 | 2 |
| 小米 | 3 |
哈希表和 Bitmap 对比
使用哈希表也同样能实现用户的去重和统计操作。
但如果使用哈希表的话,每一个用户ID 都要用整型数据存储,少则占用 4 字节(32bit),多则占用 8 字节(64bit)。而一个用户ID 在 Bitmap 中只占 1bit,内存是使用哈希表所占用内存的 1/32,甚至更少!
Bitmap 在对用户群做 交集 和 并集 运算时也有极大的便利。例如:
查找使用苹果手机的程序员用户
程序员用户(
0000000110B):num: 0 0 0 0 0 0 0 1 1 0 Bitmap: 9 8 7 6 5 4 3 2 1 0使用苹果手机的用户(
0000000010B):num: 0 0 0 0 0 0 0 0 1 0 Bitmap: 9 8 7 6 5 4 3 2 1 0使用苹果手机的程序员用户(
0000000110B & 0000000010B = 0000000010B):num: 0 0 0 0 0 0 0 0 1 0 Bitmap: 9 8 7 6 5 4 3 2 1 0查找所有男性用户或 “00后” 用户
男性用户(
0000000110B):num: 0 0 0 0 0 0 0 1 1 0 Bitmap: 9 8 7 6 5 4 3 2 1 0“00后” 用户(
0000001000B):num: 0 0 0 0 0 0 1 0 0 0 Bitmap: 9 8 7 6 5 4 3 2 1 0男性用户或 “00后” 用户(
0000000110B | 0000001000B = 0000001110B):num: 0 0 0 0 0 0 1 1 1 0 Bitmap: 9 8 7 6 5 4 3 2 1 0
这就是 Bitmap 算法的另一个优势—— 高性能的位运算。
如何利用 Bitmap 实现反向匹配。例如:想查找非 “90后” 的用户。
如果简单地做 取反运算 操作,会出现如下问题:
“90后” 用户:
num: 0 0 0 0 0 0 0 1 1 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
直接进行 非运算,得到的非 “90后” 用户:
num: 1 1 1 1 1 1 1 0 0 1
Bitmap: 9 8 7 6 5 4 3 2 1 0
显然,非 “90后” 用户实际上只有 1 个,而不是上面所得到的 8 个结果,所以不能直接进行非运算。这时可以借助一个 全量的 Bitmap。
给出 “90后” 用户的 Bitmap,再给出一个全量用户的 Bitmap。最终要求出的是存在于全量用户,但又不存在于 “90后” 用户的部分。
“90后” 用户(0000000110B):
num: 0 0 0 0 0 0 0 1 1 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
全局用户(0000001110B):
num: 0 0 0 0 0 0 1 1 1 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
使用 异或运算 进行操作,即相同位为 0,不同位为 1 得到非 “90后” 用户(0000000110B XOR 0000001110B = 0000001000B):
num: 0 0 0 0 0 0 1 0 0 0
Bitmap: 9 8 7 6 5 4 3 2 1 0
Bitmap 代码
class MyBitmap:
def __init__(self, size):
self.words = [0] * (self.get_word_index(size - 1) + 1)
self.size = size
def get_bit(self, bit_index):
if (bit_index < 0) or (bit_index > self.size - 1):
raise Exception('超过 Bitmap 有效范围!')
word_index = self.get_word_index(bit_index)
return (self.words[word_index] & (1 << bit_index)) != 0
def set_bit(self, bit_index):
if (bit_index < 0) or (bit_index > self.size - 1):
raise Exception('超过 Bitmap 有效范围!')
word_index = self.get_word_index(bit_index)
self.words[word_index] |= (1 << bit_index)
def get_word_index(self, bit_index):
# 右移 6 位,相当于除以 64
return bit_index >> 6
bitMap = MyBitmap(128)
bitMap.set_bit(126)
bitMap.set_bit(75)
print(bitMap.get_bit(126))
print(bitMap.get_bit(78))
在上述代码中,使用一个命名为 words 的 int 类型数组来存储所有的二进制位。每一个 int 元素控制其中的 64 位。(在 Python3 中,int 既可以表示整型,也可以表示长整型。)
如果要把 Bitmap 的某一位设为 1,需要经过两步:
定位到
words中的对应的int元素。通过与运算修改
int元素的值。
如果要查看 Bitmap 的某一位是否为 1,也需要经过两步:
定位到
words中的对应的int元素。判断
int元素的对应的二进制位是否为1。
LRU 算法的应用
关于用户信息的需求
需要抽出一个用户系统,向各个业务系统提供用户的基本信息。各个业务对用户信息的查询频率很高,一定要注意性能问题。
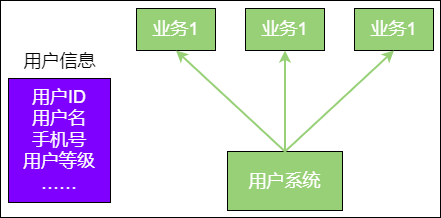
用户信息当然是存放在数据库里,但是由于对用户系统的性能要求比较高,显然不能在每一次请求时都去查询数据库。所以,在内存中创建了一个哈希表作为缓存,每当查找一个用户时会先在哈希表中进行查询,以此来提高访问的性能。
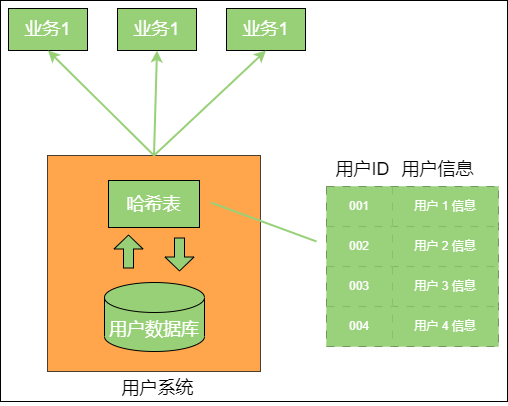
之后用户数量越来越多,当初设计的哈希表把内存给撑爆了,导致内存溢出。
解决方法
LRU(Least Recently Used) 算法,也就是最近最少使用的意思,是一种内存管理算法,该算法最早应用于 Linux 操作系统。这个算法基于一种假设:长期不被使用的数据,在未来被用到的概率也不大。因此,当数据所占内存达到一定阈值时,要移除最近最少被使用的数据。
在 LRU 算法中,使用了一种有趣的数据结构,这种数据结构叫作 哈希链表。
哈希表 是由若干个 Key-Value 组成的。在 “逻辑” 上,这些 Key-Value 是无所谓排列顺序的,谁先谁后都一样。但在 哈希链表 中,这些 Key-Value 不再是彼此无关的了,而是被一个链条串了起来。每一个 Key-Value 都具有它的 前驱 Key-Value、后继 Key-Value,就像双向链表中的节点一样。
这样,原本无序的哈希表就拥有了固定的排列顺序。依靠哈希链表的 有序性,可以把 Key-Value 按照最后的使用时间进行排序。LRU 算法的基本思路 例如:
假设使用哈希链表来缓存用户信息,目前缓存了
4个用户,这4个用户是按照被访问的时间顺序依次从链表右端插入的。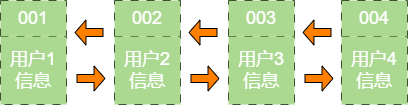
user_info_2 如果这时业务方访问用户5,由于哈希链表中没有用户5 的数据,需要从数据库中读取出来,插入缓存中。此时,链表最右端是最新被访问的用户5,最左端是最近最少被访问的用户1。
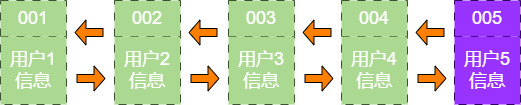
user_info_3 接下来,如果业务方访问用户2,哈希链表中已经存在用户2 的数据,这时把用户2 从它的前驱节点和后继节点之间移除,重新插入链表的最右端。此时,链表的最右端变成了最新被访问的用户2,最左端仍然是最近最少被访问的用户1。
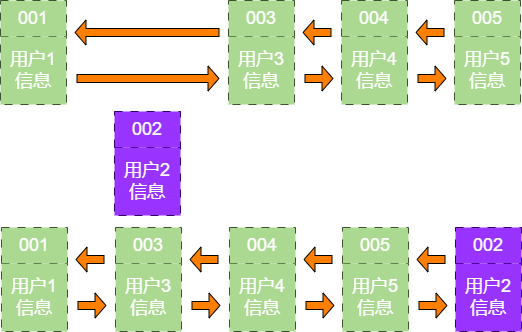
user_info_4 接下来,如果业务方请求修改用户4 的信息。同样的道理,会把用户4 从原来的位置移动到链表的最右侧,并把用户信息的值更新。这时,链表的最右端是最新被访问的用户4,最左端仍然是最近最少被访问的用户1。
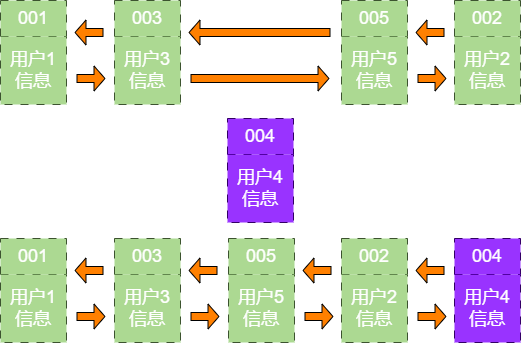
user_info_5 后来业务方又要访问用户6,用户6 在缓存里没有,需要插入哈希链表中。假设这时缓存容量已经达到上限,必须先删除最近最少被访问的数据,那么位于哈希链表最左端的用户1 就会被删除,然后再把用户6 插入最右端的位置。
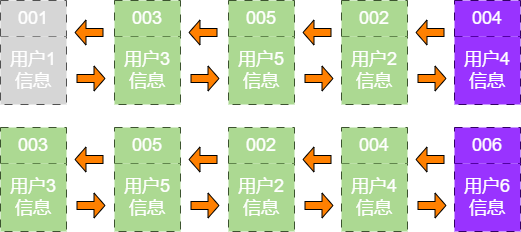
user_info_6
以上,就是 LRU 算法的基本思路。
LRU 算法代码
class LRUCache:
def __init__(self, limit):
self.limit = limit
self.hash = {}
self.head = None
self.end = None
def get(self, key):
node = self.hash.get(key)
if node is None:
return None
self.refresh_node(node)
return node.value
def put(self, key, value):
node = self.hash.get(key)
if node is None:
# 如果 key 不存在,插入 key-value
if len(self.hash) >= self.limit:
old_key = self.remove_node(self.head)
self.hash.pop(old_key)
node = Node(key, value)
self.add_node(node)
self.hash[key] = node
else:
# 如果 key 存在,刷新 key-value
node.value = value
self.refresh_node(node)
def remove(self, key):
node = self.hash.get(key)
self.remove_node(node)
self.hash.remove(key)
def refresh_node(self, node):
# 如果访问的是尾节点,无序移动节点
if node == self.end:
return
# 移除节点
self.remove_node(node)
# 重新插入节点
self.add_node(node)
def remove_node(self, node):
if (node == self.head) and (node == self.end):
# 移除唯一的节点
self.head = None
self.end = None
elif node == self.end:
# 移除节点
self.end = self.end.pre
self.end.next = None
elif node == self.head:
# 移除头节点
self.head = self.head.next
self.head.pre = None
else:
# 移除中间节点
node.pre.next = node.pre
node.next.pre = node.pre
return node.key
def add_node(self, node):
if self.end is not None:
self.end.next = node
node.pre = self.end
node.next = None
self.end = node
if self.head is None:
self.head = node
class Node:
def __init__(self, key, value):
self.key = key
self.value = value
self.pre = None
self.next = None
lruCache = LRUCache(5)
lruCache.put('001', '用户1 信息')
lruCache.put('002', '用户2 信息')
lruCache.put('003', '用户3 信息')
lruCache.put('004', '用户4 信息')
lruCache.put('005', '用户5 信息')
print(lruCache.get('002'))
lruCache.put('004', '用户4 信息更新')
lruCache.put('006', '用户6 信息')
print(lruCache.get('001'))
print(lruCache.get('006'))
A 星寻路算法
关于迷宫寻路的需求
在一个迷宫游戏中,有一些小怪物要攻击主角,现在希望给这些小怪物加上聪明的 AI(Artificial Intelligence,人工智能),让它们可以自动绕过迷宫中的障碍物,寻找到主角的所在。
解决方法
A 星寻路算法(A*search algorithm),是一种用于寻找有效路径的算法。工作过程如下:
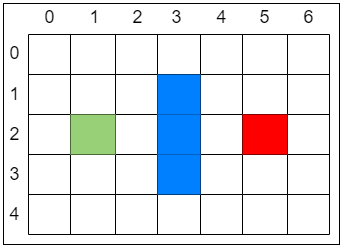
迷宫游戏的场景通常都是由小方格组成的。假设有一个 7 × 5 大小的迷宫,上图中绿色的格子是 起点,红色的格子是 终点,中间的三个蓝色格子是 一堵墙。
AI 角色从起点开始,每一步只能向上、下、左、右移动 1 格,且不能穿越墙壁。最终让 AI 角色用最少的步数到达终点。
在解决这个问题之前,先引入 2 个集合和 1 个公式。
两个集合如下:
- open_list:可到达的格子
- close_list:已到达的格子
一个公式如下:
- F = G + H
每一个格子都具有 F、G、H 这三个属性,就像下图这样。
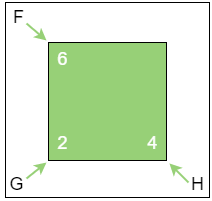
- G:从起点走到当前格子的成本也就是已经花费了多少步
- H:在不考虑障碍的情况下,从当前格子走到目标格子的距离,也就是离目标还有多远
- F:
G和H的综合评估,也就是从起点到达当前格子,再从当前格子到达目标格子的总步数,
例如:迷宫游戏让 AI 角色从起点开始,且不能穿越墙壁。最终让 AI 角色用最少的步数到达终点。
A 星寻路算法第一轮:
第一步,把起点放入 open_list,也就是刚才所说的 可到达格子 的集合。
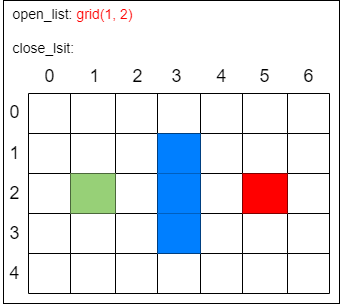
第二步,找出 open_list 中 F 值最小的方格作为当前方格。虽然没有直接计算起点方格的 F 值,但此时 open_list 中只有唯一的方格 grid(1, 2),把当前格子移出 open_list 放入 close_list。代表这个格子 已到达并检查过了。
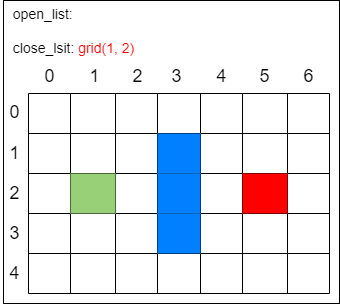
第三步,找出当前方格(刚刚检查过的格子)上、下、左、右所有可到达的格子,看它们是否在 open_list 或 close_list 当中。如果不在,则将它们加入 open_list,计算出相应的 G、H、F 值,并把当前格子作为它们的 父节点。
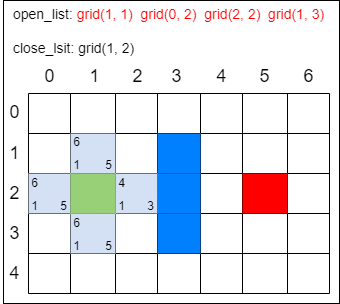
在上图中,每个格子的左下方数字是 G,右下方是 H,左上方是 F。一个格子的 “父节点” 代表它的来路,在输出最终路线时会用到。刚才经历的几个步骤是一次 局部寻路 的步骤。需要一次又一次重复刚才的第二步和第三步,直到找到终点为止。
A 星寻路算法第二轮:
第一步,找出 open_list 中 F 值最小的方格,即方格 grid(2, 2),将它作为当前方格,并把当前方格移出 open_list,放入 close_list。代表这个格子已到达并检查过了。
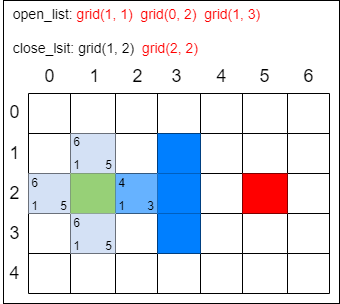
第二步,找出当前方格上、下、左、右所有可到达的格子,看它们是否在 open_list 或 close_list 当中。如果不在,则将它们加入 open_list,计算出相应的 G、H、F 值,并把当前格子作为它们的 “父节点”。
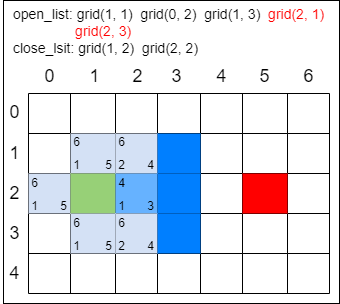
这一次 open_list 只增加了 2 个新格子。因为 grid(3, 2) 是墙壁,不用考虑,而 grid(1, 2) 在 close_list 中,说明已经检查过了,也不用考虑。
A 星寻路算法第三轮:
第一步,找出 open_list 中 F 值最小的方格。由于此时有多个方格的 F 值相等,任意选择一个即可,如将 grid(2, 3) 作为当前方格,并把当前方格移出 open_list,放入 close_list。代表这个格子已到达并检查过了。
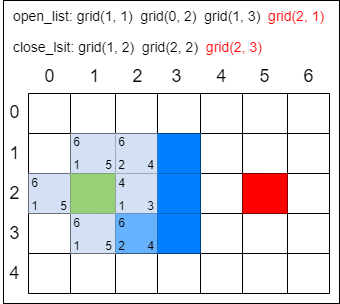
第二步,找出当前方格上、下、左、右所有可到达的格子,看它们是否在 open_list 或 close_list 当中。如果不在,则将它们加入 open_list,计算出相应的 G、H、F 值,并把当前格子作为它们的 “父节点”。
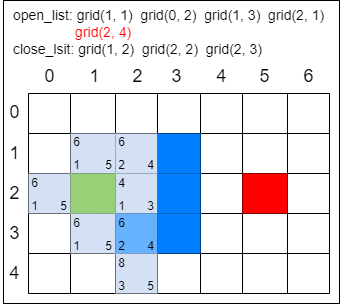
剩下的操作就是以前面的方式继续迭代,直到 open_list 中出现终点方格为止。以下操作仅用图片描述,方格中的数字表示 F 值:
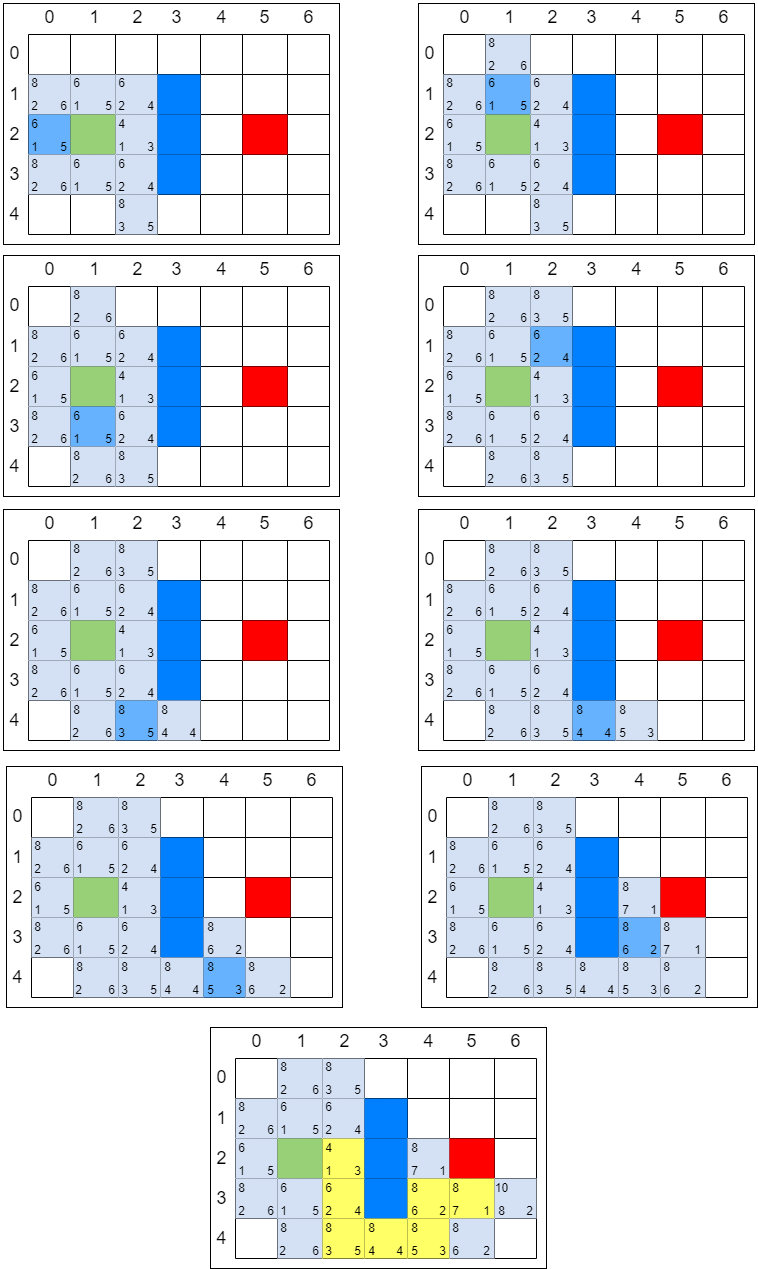
像这样一步一步来,当终点出现在 open_list 中时,寻路之旅就结束了。只要顺着终点方格找到它的 “父节点”,再找到 “父节点” 的 “父节点”……如此依次回溯,就能找到一条最佳路径了。
这就是 A 星寻路算法 的基本思想。像这样以估值高低来决定搜索优先次序的方法,被称为 启发式搜索。
A 星寻路算法代码
def a_star_search(start, end):
# 待访问的格子
open_list = []
# 已访问的格子
close_list = []
# 把起点加入 open_list
open_list.append(start)
# 主循环,每一轮检查一个当前方格节点
while len(open_list) > 0:
# 在 open_list 中查找 F 值最小的节点作为当前方格节点
current_grid = find_min_gird(open_list)
# 将当前方格节点从 open_list 中移除
open_list.remove(current_grid)
# 将当前方格节点进入 close_list
close_list.append(current_grid)
# 找到所有邻近节点
neighbors = find_neighbors(current_grid, open_list, close_list)
for grid in neighbors:
if grid not in open_list:
# 邻近节点不在 open_list 中,标记父节点 G、H、F,并放入 open_list
grid.init_grid(current_grid, end)
open_list.append(grid)
# 如果终点在 open_list 中,直接返回终点格子
for grid in open_list:
if (grid.x == end.x) and (grid.y == end.y):
return grid
# open_list 用尽,仍然找不到终点,说明终点不可到达,返回空
return None
def find_min_gird(open_list = []):
temp_grid = open_list[0]
for grid in open_list:
if grid.f < temp_grid.f:
temp_grid = grid
return temp_grid
def find_neighbors(grid, open_list = [], close_list = []):
grid_list = []
if is_valid_grid(grid.x, grid.y - 1, open_list, close_list):
grid_list.append(Grid(grid.x, grid.y - 1))
if is_valid_grid(grid.x, grid.y + 1, open_list, close_list):
grid_list.append(Grid(grid.x, grid.y + 1))
if is_valid_grid(grid.x - 1, grid.y, open_list, close_list):
grid_list.append(Grid(grid.x - 1, grid.y))
if is_valid_grid(grid.x + 1, grid.y, open_list, close_list):
grid_list.append(Grid(grid.x + 1, grid.y))
return grid_list
def is_valid_grid(x, y, open_list = [], close_list = []):
# 是否超过边界
if (x < 0) or (x >= len(MAZE)) or (y < 0) or (y >= len(MAZE[0])):
return False
# 是否有障碍物
if MAZE[x][y] == 1:
return False
# 是否已经在 open_list 中
if contain_grid(open_list, x, y):
return False
# 是否已经在 close_list 中
if contain_grid(close_list, x, y):
return False
return True
def contain_grid(grids, x, y):
for grid in grids:
if (grid.x == x) and (grid.y == y):
return True
return False
class Grid:
def __init__(self, x, y):
self.x = x
self.y = y
self.f = 0
self.g = 0
self.h = 0
self.parent = None
def init_grid(self, parent, end):
self.parent = parent
if parent is not None:
self.g = parent.g + 1
else:
self.g = 1
self.h = abs(self.x - end.x) + abs(self.y - end.y)
self.f = self.g + self.h
# 迷宫地图
MAZE = [
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
]
# 设置起点和终点
start_grid = Grid(2, 1)
end_grid = Grid(2, 5)
# 搜索迷宫终点
result_grid = a_star_search(start_grid, end_grid)
# 回溯迷宫路径
path = []
while result_grid is not None:
path.append(Grid(result_grid.x, result_grid.y))
result_grid = result_grid.parent
# 输出迷宫和路径,路径用星号表示
for i in range(0, len(MAZE)):
for j in range(0, len(MAZE[0])):
if contain_grid(path, i, j):
print('*, ', end='')
else:
print(str(MAZE[i][j]) + ', ', end='')
print()
实现红包算法
关于钱的需求
这个功能类似于微信群发红包的功能。例如,:一个人在群里发了 1 个 100 元的红包,群里有 10 个人一起来抢红包,每人抢到的金额随机分配。
红包功能需要满足以下规则:
- 所有人抢到的金额之和要等于红包金额,不能多也不能少
- 每个人至少抢到
1分钱 - 要保证红包拆分的金额尽可能分布均衡,不要出现两极分化太严重的情况
解决方法
方法1:
为了避免出现高并发引起的一些问题,每个人领取红包的金额不能在领的时候才计算,必须先计算好每个红包拆出的金额,并把它们放在一个队列里,领取红包的用户要在队列中找到属于自己的那一份。
每次拆分的金额 = 随机区间 [1分, 剩余金额 - 1分]
例如:如果分发的红包是 100 元,有 5 个人抢,那么队列第一个位置的金额在 0.01 到 99.99 元之间取随机数。
- 假设第一个位置随机得到
20元,队列第二个位置的金额要在0.01到79.99元之间取随机数 - 假设第二个位置随机得到
30元,队列第三个位置的金额要在0.01到49.99元之间取随机数 - 假设第三个位置随机得到
15元,队列第四个位置的金额要在0.01到34.99元之间取随机数 - 假设第四个位置随机得到
22元,那么第五个位置自然是35 - 22 = 13元
以这样的方式来拆分红包的话,前面拆分的金额会很大,后面的金额会越来越小!
方法2:
二倍均值法。假设剩余红包金额为 m 元,剩余人数为 n,那么有如下公式:
每次抢到的金额 = 随机区间 [0.01, m / n × 2 - 0.01] 元
这个公式,保证了每次随机金额的平均值是相等的,不会因为抢红包的先后顺序而造成不公平。
例如:假设有 5 个人,红包总额为 100 元。
100 ÷ 5 × 2 = 40,所以第 1 个人抢到的金额的随机范围是 [0.01,39.99] 元,在正常情况下,平均可以抢到 20 元。
假设第 1 个人随机抢到了 20 元,那么剩余金额是 80 元。
80 ÷ 4 × 2 = 40,所以第 2 个人抢到的金额的随机范围同样是 [0.01,39.99] 元,在正常的情况下,还是平均可以抢到 20 元。
假设第 2 个人随机抢到了 20 元,那么剩余金额是 60 元。
60 ÷ 3 × 2 = 40,所以第 3 个人抢到的金额的随机范围同样是 [0.01,39.99] 元,平均可以抢到 20 元。
以此类推,每一次抢到金额的随机范围的均值都是相等的。
提示
第 1 次随机的金额有一半概率超过 20 元,使得后面的随机金额上限不足 39.99 元;但相应地,第 1 次随机的金额同样也有一半的概率小于 20 元,使得后面的随机金额上限超过 39.99 元。因此从整体来看,第 2 次随机的金额平均范围仍然是 [0.01,39.99] 元。
这个方法虽然公平,但也存在局限性,即除最后一次外,其他每次抢到的金额都要小于剩余人均金额的 2 倍,并不是完全自由地随机抢红包。
二倍均值法代码
import random
def divide_red_package(total_amount, total_people_num):
amount_list = []
rest_amount = total_amount
rest_people_num = total_people_num
for i in range(0, total_people_num - 1):
# 随机范围:[1, 剩余人均金额的两倍),左闭右开
amount = random.randint(1, int(rest_amount / rest_people_num * 2) - 1)
rest_amount -= amount
rest_people_num -= 1
amount_list.append(amount)
amount_list.append(rest_amount)
return amount_list
my_amount_list = divide_red_package(1000, 10)
for my_amount in my_amount_list:
print("抢到金额:%.2f" % (my_amount / 100))
方法3:
线段切割法。可以把红包总金额想象成一条很长的线段,而每个人抢到的金额,是这条主线段所拆分出的若干子线段。
每一条子线段的长度,由 “切割点” 来决定。当 n 个人一起抢红包时,就需要确定 n - 1 个切割点。
因此,当 n 个人一起抢总金额为 m 元的红包时,需要做 n - 1 次随机运算,以此确定 n - 1 个切割点。随机的范围区间是 [0.01, m - 0.01]。
当所有切割点确定以后,子线段的长度也随之确定。此时红包的拆分金额,就等同于每个子线段的长度。
这就是线段切割法的思路,在这里需要注意以下两点:
注意随机切割点出现重复
尽可能降低时间复杂度和空间复杂度
