算法和数据结构
算法
算法(algorithm) 是一个很古老的概念,最早来自数学领域。
有一个关于算法的小故事,估计大家都有耳闻
在很久很久以前,曾经有一个顽皮又聪明的 “熊孩子”,天天在课堂上调皮捣蛋。
一次数学课上,老师为了让他们安静下来,给他们列了一道很难的算式,让他们一个小时内算出 1 + 2 + 3 + …… + 100 的得数。
老师以为,孩子们会按部就班地一步一步计算,就像下面这样:
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
...
全班只有 “熊孩子” 用了不到 20 分钟给出了答案,因为他想到了用以下方法计算:
1 + 100 = 101
2 + 99 = 101
3 + 98 = 101
4 + 97 = 101
...
一共有 50 个 101 ,所以 50 × 101 就是 1 加到一百的得数。可以这样来计算:
(1 + 100) × 100 ÷ 2 = 5 050
这个 “熊孩子” 就是后来著名的犹太数学家 约翰·卡尔·弗里德里希·高斯,而他所采用的这种 等差数列求和 的方法,被称为 高斯算法。(上文的故事情节与史实略有出入。)
这是数学领域中算法的一个简单示例。在数学领域里,算法是用于解决某一类问题的公式和思想。
而计算机科学领域的算法,它的本质是一系列程序指令,用于解决特定的运算和逻辑问题。
从宏观上来看,数学领域的算法和计算机领域的算法有很多相通之处。
算法有简单的,也有复杂的
- 简单的算法:例如:给出一组整数,找出其中最大的数
- 复杂的算法:例如:在多种物品里选择装入背包的物品,使背包里的物品总价值最大;或找出从一个城市到另一个城市的最短路线
算法有高效的,也有拙劣的
例如:刚才讲的从 1 加到 100。
- 高效的算法:高斯利用等差数列的规律,省时省力地求出了最终结果。显然是更加高效的算法
- 拙劣的算法:老师心中所想的算法,按部就班地一个数一个数进行累加。虽然这种算法也能得到最终结果,但是其计算过程要低效得多
衡量算法好坏的重要标准有两个
- 时间复杂度
- 空间复杂度
数据结构
数据结构(data structure) 是数据的组织、管理和存储格式,其使用目的是为了高效地访问和修改数据。
提示
数据结构是算法的基石。如果把算法比喻成美丽灵动的舞者,那么数据结构就是舞者脚下广阔而坚实的舞台。
数据结构的组成方式:
线性结构
线性结构是最简单的数据结构,包括数组、链表,以及由它们衍生出来的栈、队列、哈希表。
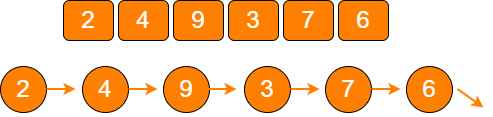
linear 树
树是相对复杂的数据结构,其中比较有代表性的是二叉树,由它又衍生出了二叉堆之类的数据结构。
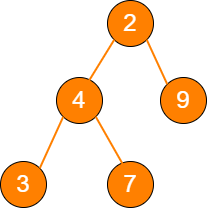
tree 图
图是更为复杂的数据结构,因为在图中会呈现出多对多的关联关系。
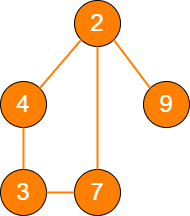
picture 其他数据结构
还有一些其他的千奇百怪的数据结构。它们由基本数据结构变形而来,用于解决某些特定问题,如跳表、哈希链表、位图等。
有了数据结构这个舞台,算法才可以尽情舞蹈。在解决问题时,不同的算法会选用不同的数据结构。例如:排序算法中的堆排序,利用的就是二叉堆这样一种数据结构;再如缓存淘汰算法 LRU(Least Recently Used,最近最少使用),利用的就是特殊数据结构哈希链表。
时间复杂度
时间复杂度 是对一个算法运行时间长短的量度,用大 O 表示,记作 T(n)=O(f(n))。
提示
时间复杂度 是执行算法的时间成本
基本操作执行次数
提示
由于受运行环境和输入规模的影响,代码的绝对执行时间是无法预估的。但却可以预估代码的基本操作执行次数
关于代码的基本操作执行次数,下面用生活中的四个场景来进行说明。
场景一
一个长度为
10cm的面包,每3分钟吃掉1cm,那么吃掉整个面包需要多久?答案自然是
3 × 10即30分钟。如果面包的长度是
n cm呢?此时吃掉整个面包,需要3乘以n即3n分钟。如果用一个函数来表达吃掉整个面包所需要的时间,可以记作 T(n)=3n,
n为面包的长度。场景二
一个长度为
16cm的面包,每5分钟吃掉面包剩余长度的一半,即第5分钟吃掉8cm,第10分钟吃掉4cm,第15分钟吃掉2cm…… 那么把面包吃得只剩1cm需要多久?这个问题用数学方式表达就是,数字
16不断地除以2,那么除几次以后的结果等于1?这里涉及数学中的对数,即以2为底16的对数 log216。因此,把面包吃得只剩下
1cm,需要 5 × log216 即20分钟。如果面包的长度是
n cm呢?此时,需要5乘以 log2n 即 5log2n 分钟,记作 T(n)=5log2n。场景三
一个长度为
10cm的面包和一个鸡腿,每2分钟吃掉1个鸡腿。那么吃掉整个鸡腿需要多久?答案自然是
2分钟。因为这里只要求吃掉鸡腿,和10cm的面包没有关系。如果面包的长度是
n cm呢?无论面包多长,吃掉鸡腿的时间都是2分钟,记作 T(n)=2。场景四:
一个长度为
10cm的面包,吃掉第一个1cm需要1分钟时间,吃掉第二个1cm需要2分钟时间,吃掉第三个1cm需要3分钟时间…… 每吃1cm所花的时间就比吃上一个1cm多用1分钟。那么吃掉整个面包需要多久?答案是从
1累加到10的总和,也就是55分钟。如果面包的长度是
n cm呢?根据高斯算法,此时吃掉整个面包需要1 + 2 + 3 + …… + n即(1 + n) × n / 2分钟,也就是 0.5n2 + 0.5n 分钟,记作 T(n)=0.5n2 + 0.5n。
上面所讲的是吃东西所花费的时间,这一思想同样适用于对程序 基本操作执行次数 的统计。设 T(n) 为程序基本操作执行次数的函数(也可以认为是程序的相对执行时间函数),n 为输入规模。
刚才的四个场景分别对应了程序中最常见的四种执行方式。
场景一:T(n)=3n
执行次数是 线性 的。
def eat1(n): for i in range(n): print("等待 1 分钟") print("等待 1 分钟") print("吃 1cm 面包")场景二:T(n)=5log2n
执行次数是用 对数 计算的。
def eat2(n): while n > 1: print("等待 1 分钟") print("等待 1 分钟") print("等待 1 分钟") print("等待 1 分钟") print("吃一半面包") n /= 2场景三:T(n)=2
执行次数是 常量。
def eat3(n): print("等待 1 分钟") print("吃 1 个鸡腿")场景四:T(n)=0.5n2 + 0.5n
执行次数是用 多项式 计算的。
def eat4(n): for i in range(n): for j in range(i): print("等待 1 分钟") print("吃 1cm 面包")
渐进时间复杂度
若存在函数 f(n),使得当 n 趋近于无穷大时,T(n)/f(n) 的极限值为不等于零的常数,则称 f(n) 是 T(n) 的同数量级函数。记作 T(n)=O(f(n)),称为 O(f(n)),O 为算法的 渐进时间复杂度,简称为 时间复杂度。
因为渐进时间复杂度用大写 O 来表示,所以也被称为 大 O 表示法。
提示
时间复杂度就是把程序的相对执行时间函数 T(n) 简化为一个数量级,这个数量级可以是 n、n2、n3 等
推导出时间复杂度有如下几个原则:
- 如果运行时间是常数量级,则用常数
1表示 - 只保留时间函数中的最高阶项
- 如果最高阶项存在,则省去最高阶项前面的系数
刚才的四个场景对应的时间复杂度。
场景一:T(n)=3n
最高阶项为
3n,省去系数3,则转化的时间复杂度为:T(n)=O(n)。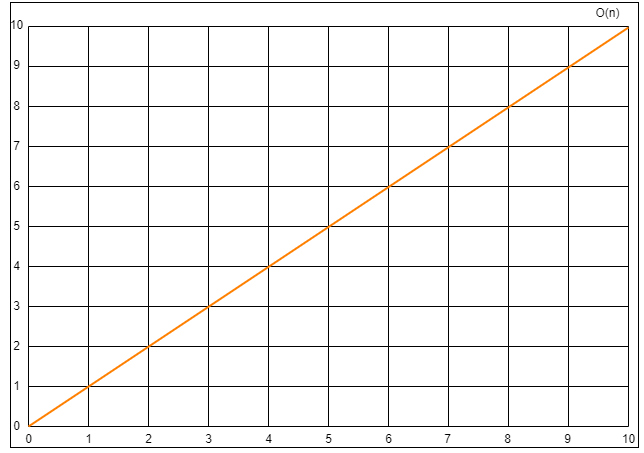
T(n)=O(n) 场景二:T(n)=5log2n
最高阶项为 5log2n,省去系数
5,则转化的时间复杂度为:T(n)=O(log2n)。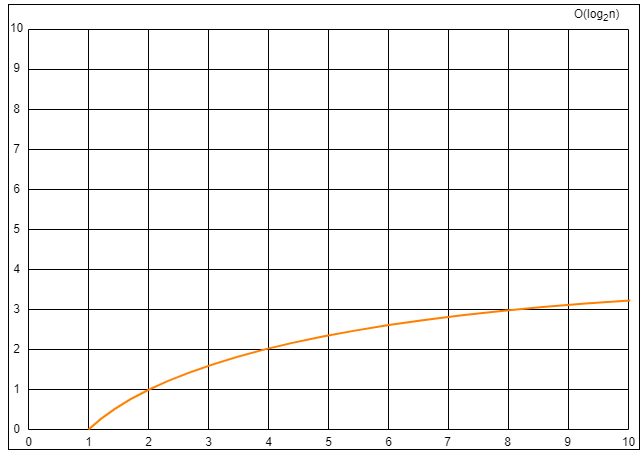
T(n)=O(log2n) 场景三:T(n)=2
只有常数量级,则转化的时间复杂度为:T(n)=O(1)。
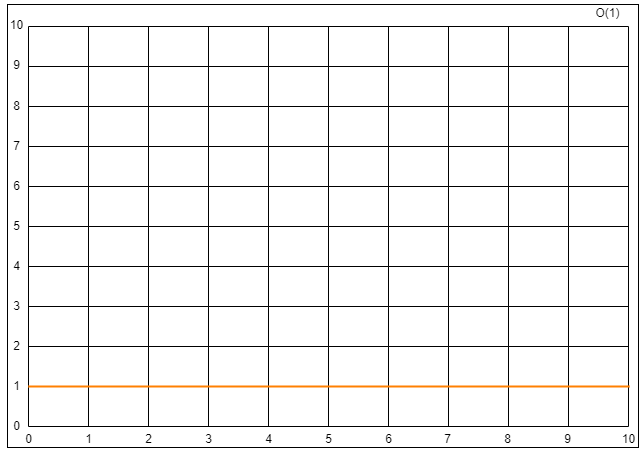
T(n)=O(1) 场景四:T(n)=0.5n2 + 0.5n
最高阶项为 0.5n2,省去系数
0.5,则转化的时间复杂度为:T(n)=O(n2)。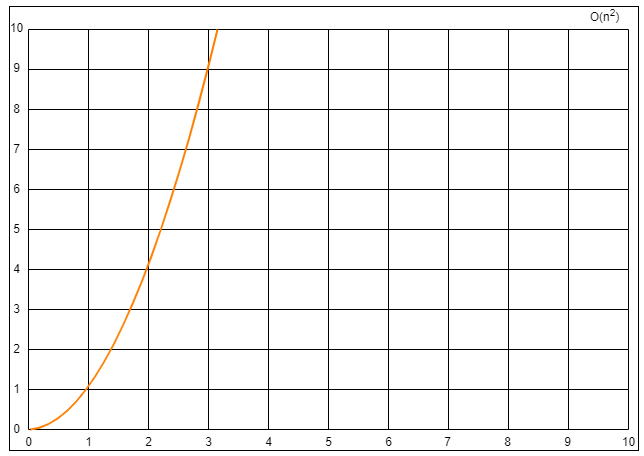
T(n)=O(n2)
这四种时间复杂度对程度执行用时时间由低到高为:
O(1) < O(log2n) < O(n) < O(n2)
相关信息
在编程的世界中有各种各样的算法,除了上述四个场景,还有许多不同形式的时间复杂度,例如:O(nlog2n)、O(n3)、O(mn)、O(2n)、O(n!)
时间复杂度的巨大差异
算法A 的执行次数是 T(n)=100n,时间复杂度是 O(n)。
算法B 的执行次数是 T(n)=5n2,时间复杂度是 O(n2)。
算法A 运行在老旧电脑上,算法B 运行在某台超级计算机上,超级计算机的运行速度是老旧电脑的 100 倍。
那么,随着输入规模 n 的增长,两种算法谁运行速度更快呢?
| n(规模) | T(n) = 100n x 100 | T(n) = 5n2 |
|---|---|---|
| n = 1 | 10 000 | 5 |
| n = 5 | 50 000 | 125 |
| n = 10 | 100 000 | 500 |
| n = 100 | 1 000 000 | 50 000 |
| n = 1 000 | 10 000 000 | 5 000 000 |
| n = 10 000 | 100 000 000 | 500 000 000 |
| n = 100 000 | 1 000 000 000 | 50 000 000 000 |
| n = 1 000 000 | 10 000 000 000 | 5 000 000 000 000 |
从上面的表格可以看出,当 n 的值很小时,算法A 的运行用时要远大于算法B;当 n 的值在 1 000 左右时,算法A 和算法B 的运行时间已经比较接近;随着 n 的值越来越大,甚至达到十万、百万时,算法A 的优势开始显现出来,算法B 的运行速度则越来越慢,差距越来越明显。这就是不同时间复杂度带来的差距。
空间复杂度
和时间复杂度类似,空间复杂度 是对一个算法在运行过程中临时占用存储空间大小的量度,它同样使用了 大 O 表示法。
程序占用空间大小的计算公式记作 S(n)=O(f(n)),其中 n 为问题的规模,f(n) 为算法所占存储空间的函数。
提示
空间复杂度 是执行算法的空间成本
空间复杂度的计算
常见的空间复杂度有下面几种情形:
常量空间
当算法的存储空间大小固定,和输入规模没有直接的关系时,空间复杂度记作 O(1)。例如:
def fun1(n): i = 3 # do something线性空间
当算法分配的空间是一个线性的集合(如:数组),并且集合大小和输入规模
n成正比时,空间复杂度记作 O(n)。例如:def fun2(n): my_arrary = [[0] * n] # do something二维空间
当算法分配的空间是一个二维数组集合,并且集合的长度和宽度都与输入规模
n成正比时,空间复杂度记作 O(n2)。例如:def fun3(n): matrix = [[0] * n] * n # do something递归空间
递归是一个比较特殊的场景。虽然递归代码中并没有显式地声明变量或集合,但是计算机在执行程序时,会专门分配一块内存,用来存储 方法调用栈。
方法调用栈包括 进栈 和 出栈 两个行为。
当进入一个新方法时,执行进栈操作,把调用的方法和参数信息压入栈中;当方法返回时,执行出栈操作,把调用的方法和参数信息从栈中弹出。例如:
def fun4(n): if n > 0: fun4(n - 1) # do something执行递归操作所需要的内存空间和递归的深度成正比。纯粹的递归操作的空间复杂度也是线性的,如果递归的深度是
n,那么空间复杂度就是 O(n)。
常见的空间复杂度按照从低到高的顺序为:
O(1) < O(n) < O(n2) 等。
其中递归算法的空间复杂度和递归深度成正比。
时间与空间的取舍
在绝大多数时候,时间复杂度更为重要一些,宁可多分配一些内存空间,也要提升程序的执行速度。
