面试中的算法
判断链表有环
题目
有一个单向链表,链表中有可能出现 “环”,就像下图这样。那么,如何用程序来判断该链表是否为有环链表。

解题思路
方法1:
首先从头节点开始,依次遍历单链表中的每一个节点。每遍历一个新节点,就从头检查新节点之前的所有节点,用新节点和此节点之前所有节点依次做比较。如果发现新节点和之前的某个节点相同,则说明该节点被遍历过两次,链表有环;如果之前的所有节点中不存在与新节点相同的节点,就继续遍历下一个新节点,继续重复刚才的操作。
相关信息
假设链表的节点数量为 n,则该解法的时间复杂度为 O(n2)。由于并没有创建额外的存储空间,所以空间复杂度为 O(1)
方法2:
首先创建一个以节点ID 为 Key 的 set 集合,用来存储曾经遍历过的节点。然后同样从头节点开始,依次遍历单链表中的每一个节点。每遍历一个新节点,都用新节点和 set 集合中存储的节点进行比较,如果发现 set 中存在与之相同的节点ID,则说明链表有环,如果 set 中不存在与新节点相同的节点ID,就把这个新节点ID 存入 set 中,之后进入下一节点,继续重复刚才的操作。
相关信息
假设链表的节点数量为 n,则该解法的时间复杂度是 O(n)。由于使用了额外的存储空间,所以算法的空间复杂度同样是 O(n)
方法3:
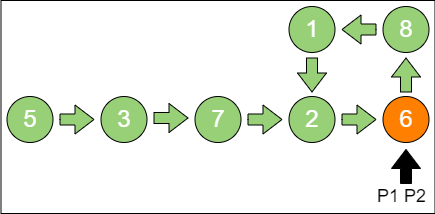
首先创建两个指针 p1 和 p2(在 Python 里就是两个对象引用),让它们同时指向这个链表的头节点。然后开始一个大循环,在循环体中,让指针 p1 每次向后移动一个节点,让指针 p2 每次向后移动两个节点,然后比较两个指针指向的节点是否相同。如果相同,则可以判断出链表有环,如果不同,则继续下一次循环。
第 1 步,p1 和 p2 都指向节点5。
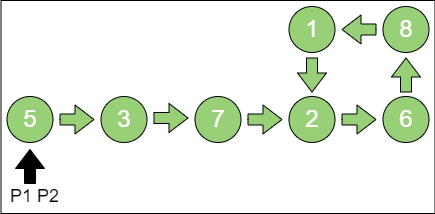
第 2 步,p1 指向节点3,p2 指向节点7。
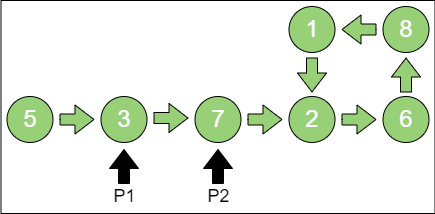
第 3 步,p1 指向节点7,p2 指向节点6。
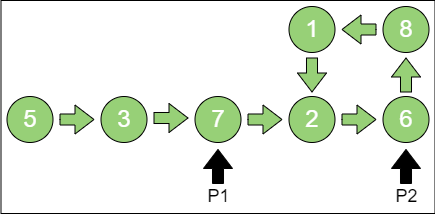
第 4 步,p1指向节点2,p2指向节点1。
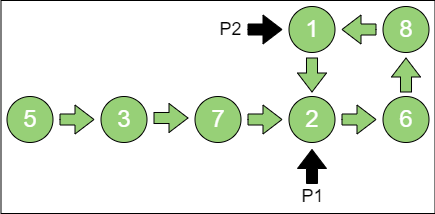
第 5 步,p1指向节点6,p2也指向节点6,p1 和 p2 所指相同,说明链表有环。
相关信息
假设链表的节点数量为 n,则该算法的时间复杂度为 O(n)。除两个指针外,没有使用任何额外的存储空间,所以空间复杂度是 O(1)
代码
class Node:
def __init__(self, data):
self.data = data
self.next = Node
def is_cycle(head):
p1 = head
p2 = head
while p2 is not None and p2.next is not None:
p1 = p1.next
p2 = p2.next.next
if p1 == p2:
return True
return False
node1 = Node(5)
node2 = Node(3)
node3 = Node(7)
node4 = Node(2)
node5 = Node(6)
node1.next = node2
node2.next = node3
node3.next = node4
node4.next = node5
node5.next = node2
print(is_cycle(node1))
问题扩展
扩展问题1:如果链表有环,如何求出环的长度?
当两个指针首次相遇,证明链表有环的时候,让两个指针从相遇点继续循环前进,并统计前进的循环次数,直到两个指针第 2 次相遇。此时,统计出来的前进次数就是环长。
因为指针 p1 每次走一步,指针 p2 每次走两步,两者的速度差是一步。当两个指针再次相遇时,p2 比 p1 多走了整整一圈。因此,环长 = 每一次速度差 × 前进次数 = 前进次数。
扩展问题2:如果链表有环,如何求出入环节点?
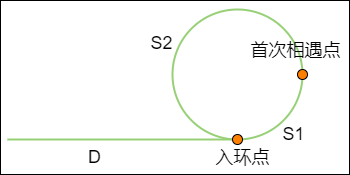
假设从链表头节点到入环点的距离是 D,从入环点到两个指针首次相遇点的距离是 S1,从首次相遇点回到入环点的距离是 S2。
那么,当两个指针首次相遇时,各自所走的距离是多少呢?
指针 p1 一次只走一步,所走的距离是 D + S1。
指针 p2 一次走两步,多走了 n(n >= 1) 整圈,所走的距离是 D + S1 + n(S1 + S2)。
由于 p2 的速度是 p1 的两倍,所以所走距离也是 p1 的两倍,因此:2(D + S1) = D + S1 + n(S1 + S2),等式经过整理得出:D = (n - 1)(S1 + S2) + S2
也就是说,从链表头节点到入环点的距离,等于从首次相遇点绕环 n - 1 圈再回到入环点的距离。
这样一来,只要把其中一个指针放回到头节点位置,另一个指针保持在首次相遇点,两个指针都是每次向前走一步。那么,它们最终相遇的节点,就是入环节点。
最小栈的实现
题目
实现一个栈,该栈带有出栈(pop)、入栈(push)、取最小元素(get_min)三个方法。要保证这三个方法的时间复杂度都是 O(1)。
解题思路
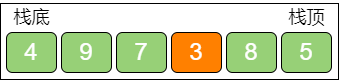
第 1 步,设原有的栈叫作栈A,此时创建一个额外的 “备胎” 栈B,用于辅助栈A。
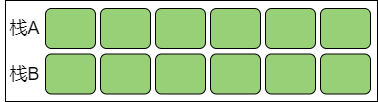
第 2 步,当第一个元素进入栈A 时,让新元素也进入栈B。这个唯一的元素是栈A 的当前最小值。
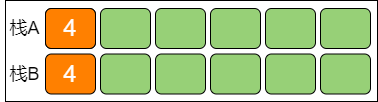
第 3 步,之后,每当新元素进入栈A 时,比较新元素和栈A 当前最小值的大小,如果小于栈A 当前最小值,则让新元素进入栈B,此时栈B 的栈顶元素就是栈A 当前最小值。
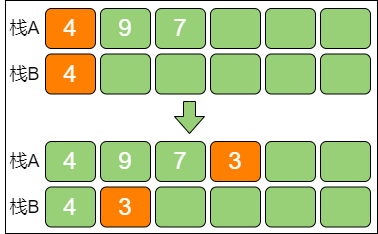
第 4 步,每当栈A 有元素出栈时,如果出栈元素是栈A 当前最小值,则让栈B 的栈顶元素也出栈。此时栈B 余下的栈顶元素所指向的是栈A 中原本第二小的元素,代替刚才的出栈元素成为栈A 的当前最小值。
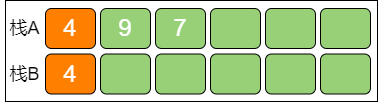
第 5 步,当调用 get_min 方法时,返回栈B 的栈顶所存储的值,这也是栈A 的最小值。
显然,这个解法中进栈、出栈、取最小值的时间复杂度都是 O(1),最坏情况空间复杂度是 O(n)。
代码
class MinStack:
def __init__(self):
self.main_stack = []
self.min_stack = []
def push(self, element):
self.main_stack.append(element)
# 若辅助栈为空,或新元素的值小于或等于辅助栈栈顶元素的值,将新元素压入辅助栈
if (len(self.min_stack) == 0) or (element <= self.min_stack[len(self.min_stack) - 1]):
self.min_stack.append(element)
def pop(self):
# 如果出栈元素和辅助栈栈顶元素的值相等,辅助栈的栈顶元素出栈
if self.main_stack[len(self.main_stack) - 1] == self.min_stack[len(self.min_stack) - 1]:
self.min_stack.pop()
return self.main_stack.pop()
def get_min(self):
if len(self.main_stack) == 0:
return None
return self.min_stack[len(self.min_stack) - 1]
my_stack = MinStack()
my_stack.push(4)
my_stack.push(9)
my_stack.push(7)
my_stack.push(3)
my_stack.push(8)
my_stack.push(5)
print(my_stack.get_min())
my_stack.pop()
my_stack.pop()
my_stack.pop()
print(my_stack.get_min())
求出最大公约数
题目
写一段代码,求出两个整数的最大公约数,要尽量优化算法的性能。
解题思路
方法1:
使用 “暴力枚举” 的方法,从较小整数的一半开始,试图找到一个合适的整数 i,看看这个整数能否被 a 和 b 同时整除。
相关信息
时间复杂度是 O(min(a, b))
代码
def get_greatest_common_divisor(a, b):
big = max(a, b)
small = min(a, b)
if big % small == 0:
return small
for i in range(small // 2, 1, -1):
if small % i == 0 and big % i == 0:
return i
return 1
print(get_greatest_common_divisor(25, 5))
print(get_greatest_common_divisor(100, 75))
print(get_greatest_common_divisor(99, 55))
方法2:
相关信息
辗转相除法,又名 欧几里得算法(Euclidean algorithm),该算法的目的是求出两个正整数的最大公约数。它是已知最古老的算法,其产生时间可追溯至公元前 300 年。
这条算法基于一个定理:两个正整数 a 和 b(a > b),它们的最大公约数等于 a 除以 b 的余数 c 和 b 之间的最大公约数。例如:10 和 25,25 除以 10 商 2 余 5,那么 10 和 25 的最大公约数,等于 10 和 5 的最大公约数。
相关信息
时间复杂度可以近似为 O(log(max(a, b))),但是取模运算性能较差
首先,计算出 a 除以 b 的余数 c,把问题转化成求 b 和 c 的最大公约数;然后计算出 b 除以 c 的余数 d,把问题转化成求 c 和 d 的最大公约数;再计算出 c 除以 d 的余数 e,把问题转化成求 d 和 e 的最大公约数……
以此类推,逐渐把两个较大整数之间的运算简化成两个较小整数之间的运算,直到两个数可以整除,或者其中一个数减小到 1 为止。
代码
def get_greatest_common_divisor_v2(a, b):
big = max(a, b)
small = min(a, b)
if big % small == 0:
return small
return get_greatest_common_divisor_v2(big % small, small)
print(get_greatest_common_divisor_v2(25, 5))
print(get_greatest_common_divisor_v2(100, 75))
print(get_greatest_common_divisor_v2(99, 55))
当两个整数较大时,做 a % b 取模运算的性能会比较差。这时需要用到另一个算法 更相减损术。
方法3:
相关信息
更相减损术 出自中国古代的 《九章算术》,也是一种求最大公约数的算法。
它的原理更加简单:两个正整数 a 和 b(a > b),它们的最大公约数等于 a - b 的差值 c 和较小数 b 的最大公约数。例如:10 和 25,25 减 10 的差是 15,那么 10 和 25 的最大公约数,等同于 10 和 15 的最大公约数。
相关信息
避免了取模运算,但是算法性能不稳定,最坏时间复杂度为 O(max(a, b))
由此,同样可以通过递归来简化问题。首先,计算出 a 和 b 的差值 c(假设 a > b),把问题转化成求 b 和 c 的最大公约数;然后计算出 c 和 b 的差值 d(假设 c > b),把问题转化成求 b 和 d 的最大公约数;再计算出 b 和 d 的差值 e(假设 b > d),把问题转化成求 d 和 e 的最大公约数……
以此类推,逐渐把两个较大整数之间的运算简化成两个较小整数之间的运算,直到两个数相等为止,最大公约数就是最终相等的这两个数的值。
代码
def get_greatest_common_divisor_v3(a, b):
if a == b:
return a
big = max(a, b)
small = min(a, b)
return get_greatest_common_divisor_v3(big - small, small)
print(get_greatest_common_divisor_v3(25, 5))
print(get_greatest_common_divisor_v3(100, 75))
print(get_greatest_common_divisor_v3(99, 55))
更相减损术依靠两数求差的方式来递归,运算次数远大于辗转相除法的取模方式。
更相减损术是不稳定的算法,当两数相差悬殊时,如计算 10000 和 1 的最大公约数,就要递归 9999 次!
方法4:
把 辗转相除法 和 更相减损术 的优势结合起来,在更相减损术的基础上使用 移位运算。
相关信息
不但避免了取模运算,而且算法性能稳定,时间复杂度为 O(log(max(a, b)))
众所周知,移位运算的性能非常好。对于给出的正整数 a 和 b,不难得到如下的结论:
(下面获得最大公约数的方法 get_greatest_common_divisor 简写为 gcd。)
- 当
a和b均为偶数时,gcd(a, b) = 2 × gcd(a / 2, b / 2) = 2 × gcd(a >> 1, b >> 1) - 当
a为偶数,b为奇数时,gcd(a, b) = gcd(a / 2, b) = gcd(a >> 1, b) - 当
a为奇数,b为偶数时,gcd(a, b) = gcd(a, b / 2) = gcd(a , b >> 1) - 当
a和b均为奇数时,先利用更相减损术运算一次,gcd(a, b) = gcd(b, a - b),此时a - b必然是偶数,然后又可以继续进行移位运算
例如:计算 10 和 25 的最大公约数的步骤如下:
整数
10通过移位,可以转换成求5和25的最大公约数。利用更相减损术,计算出
25 - 5 = 20,转换成求5和20的最大公约数。整数
20通过移位,可以转换成求5和10的最大公约数。整数
10通过移位,可以转换成求5和5的最大公约数。利用更相减损术,因为两数相等,所以最大公约数是
5。
这种方式在两数都比较小时,可能看不出计算次数的优势;当两数越大时,计算次数的减少就会越明显。
代码
def get_greatest_common_divisor_v4(a, b):
if a == b:
return a
if (a & 1) == 0 and (b & 1) == 0:
return get_greatest_common_divisor_v4(a >> 1, b >> 1) << 1
elif (a & 1) == 0 and (b & 1) != 0:
return get_greatest_common_divisor_v4(a >> 1, b)
elif (a & 1) != 0 and (b & 1) == 0:
return get_greatest_common_divisor_v4(a, b >> 1)
else:
big = max(a, b)
small = min(a, b)
return get_greatest_common_divisor_v4(big - small, small)
print(get_greatest_common_divisor_v4(25, 5))
print(get_greatest_common_divisor_v4(100, 75))
print(get_greatest_common_divisor_v4(99, 55))
在上述代码中,判断整数奇偶性的方式是让整数和 1 进行与运算,如果 (a & 1) == 0,则说明整数 a 是偶数;如果 (a & 1) != 0,则说明整数 a 是奇数。
判断一个数是否为 2 的整数次幂
题目
一个正整数,如何判断它是不是 2 的整数次幂?
实现一个方法,来判断一个正整数是否是 2 的整数次幂(如:16 是 2 的 4 次方,返回 true;18 不是 2 的整数次幂,则返回 false),要求性能尽可能高。
解题思路
方法1:
创建一个中间变量 temp,初始值是 1。然后进入一个循环,每次循环都让 temp 乘以 2,并和目标整数相比较,如果相等,则说明目标整数是 2 的整数次幂;如果不相等,则让 temp 增大一倍,继续循环并进行比较。当 temp 的值大于目标整数时,说明目标整数不是 2 的整数次幂。
相关信息
如果目标整数的大小是 n,则此方法的时间复杂度是 O(log2n)
代码
def is_power_of_2(num):
temp = 1
while temp <= num:
if temp == num:
return True
temp = temp * 2
return False
print(is_power_of_2(19))
print(is_power_of_2(32))
方法2:
将乘法操作改成向左移位,移位的性能比乘法高。这样确实有一定优化。但目前算法的时间复杂度仍然是 O(log2n),本质上没有变。
代码
def is_power_of_2_v2(num):
temp = 1
while temp <= num:
if temp == num:
return True
temp = temp << 1
return False
print(is_power_of_2_v2(19))
print(is_power_of_2_v2(32))
方法3:
如果把 2 的整数次幂转换成二进制数时,只有最高位是 1,其他位都是 0。
| 十进制数 | 二进制数 | 是否为 2 的整数次幂 |
|---|---|---|
| 8 | 1 000B | 是 |
| 16 | 10 000B | 是 |
| 32 | 100 000B | 是 |
| 64 | 1 000 000B | 是 |
| 100 | 1 100 100B | 否 |
接下来,如果把这些 2 的整数次幂各自减 1,再转化成二进制数时,它的二进制数的数字就全部变成了 1。
| 十进制数 | 二进制数 | 原数值 - 1 | 是否为 2 的整数次幂 |
|---|---|---|---|
| 8 | 1 000B | 111B | 是 |
| 16 | 10 000B | 1 111B | 是 |
| 32 | 100 000B | 11 111B | 是 |
| 64 | 1 000 000B | 111 111B | 是 |
| 100 | 1 100 100B | 1 100 011B | 否 |
这时候如果用原数值(2 的整数次幂)和它减 1 的结果进行按位与运算,也就是 n & (n - 1)。0 和 1 按位与运算的结果是 0,所以凡是 2 的整数次幂和它本身减 1 的结果进行与运算,结果都必定是 0。反之,如果一个整数不是 2 的整数次幂,结果一定不是 0。
| 十进制数 | 二进制数 | 原数值 - 1 | n & (n -1) | 是否为 2 的整数次幂 |
|---|---|---|---|---|
| 8 | 1 000B | 111B | 0 | 是 |
| 16 | 10 000B | 1 111B | 0 | 是 |
| 32 | 100 000B | 11 111B | 0 | 是 |
| 64 | 1 000 000B | 111 111B | 0 | 是 |
| 100 | 1 100 100B | 1 100 011B | 1 100 000B | 否 |
相关信息
所以对于一个整数 n,只需要计算 n & (n - 1) 的结果是不是 0。这个方法的时间复杂度只有 O(1)
代码
def is_power_of_2_v3(num):
return (num & (num - 1)) == 0
print(is_power_of_2_v3(19))
print(is_power_of_2_v3(32))
无序数组排序后的最大相邻差
题目
有一个无序整型数组,如何求出该数组排序后的任意两个相邻元素的最大差值?要求时间复杂度和空间复杂度尽可能低。例如:
无序数组:2 6 3 4 5 10 9
排序结果:2 3 4 5 6 9 10
最大相邻差为 9 - 6 = 3
解题思路
方法1:
使用任意一种时间复杂度为 O(nlog2n) 的排序算法(如:快速排序)给原数组排序,然后遍历排好序的数组,并对每两个相邻元素求差,最终得到最大差值。
相关信息
该解法的时间复杂度是 O(nlog2n),在不改变原数组的情况下,空间复杂度是 O(n)
方法2:
利用 计数排序 的思想,先求出原数组中的 最大值(max) 与 最小值(min) 的区间长度
k(k = max - min + 1),以及偏移量d = min。创建一个长度为
k的新 数组(Array)。遍历原数组,每遍历一个元素,就把新数组
Array对应下标的值加1。例如:原数组元素的值为n,则将Array[n - min]的值加1。遍历结束后,Array的一部分元素的值变成了1或更高的数值,一部分元素的值仍然是0。遍历新数组
Array,统计出Array中最大连续出现0值的次数加1,即为相邻元素最大差值。
例如:给定一个无序数组 {2, 6, 3, 4, 5, 10, 9},处理过程如下。
第一步,确定 k(数组长度)和 d(偏移量)。
min = 2
max = 10
k = max - min + 1 = 10 - 2 + 1 = 9
d = min = 2
第二步,创建数组。
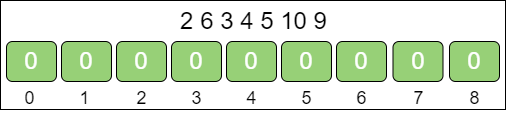
第三步,遍历原数组,对号入座。
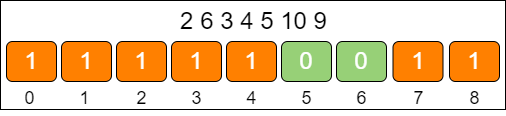
第四步,判断 0 值最多连续出现的次数,计算出最大相邻差。
最大相邻差:7 - 4 = 3
注
如果原数组只有 3 个元素:1、2、1000000,那就要创建长度是 1000000 的数组
方法3:
利用 桶排序 的思想,根据原数组的长度
n,创建出n个桶,每一个桶代表一个区间范围。其中第一个桶从原数组的最小值min_value开始,区间跨度是(max_value - min_value) / (n - 1)。遍历原数组,把原数组中的每一个元素插入对应的桶中,记录每一个桶的最大值和最小值。
遍历所有的桶,统计出每一个桶的最大值,和这个桶右侧非空桶的最小值的差,数值最大的差即为原数组排序后的相邻最大差值。
例如:给出一个无序数组 {2, 6, 3, 4, 5, 10, 9},处理过程如下。
第一步,根据原数组,创建桶,确定每个桶的区间范围。

第二步,遍历原数组,确定每个桶内的最大和最小值。

第三步,遍历所有的桶,找出最大相邻差。
最大相邻差:9 - 6 = 3
相关信息
这个方法不需要像标准桶排序那样在每一个桶内部进行排序,只需要记录桶内的最大值和最小值即可,所以时间复杂度稳定在 O(n)
代码
class Bucket:
def __init__(self):
self.min = None
self.max = None
def get_max_sorted_distance(array = []):
# 1. 得到数列的最大值和最小值
max_value = array[0]
min_value = array[0]
for i in range(1, len(array)):
if array[i] > max_value:
max_value = array[i]
if array[i] < min_value:
min_value = array[i]
d = max_value - min_value
# 如果 max_value 和 min_value 相等,说明数组所有元素都相等,返回 0
if d == 0:
return 0
# 2. 初始化桶
bucket_num = len(array)
buckets = []
for i in range(0, bucket_num):
buckets.append(Bucket())
# 3. 遍历原始数组,确定每个桶的最大值和最小值
for i in range(0, len(array)):
# 确定数组元素所归属的桶下标
index = int((array[i] - min_value) * (bucket_num - 1) / d)
if buckets[index].min is None or buckets[index].min > array[i]:
buckets[index].min = array[i]
if buckets[index].max is None or buckets[index].max < array[i]:
buckets[index].max = array[i]
# 4. 遍历桶,找到最大差值
left_max = buckets[0].max
max_distance = 0
for i in range(1, len(buckets)):
if buckets[i].min is None:
continue
if buckets[i].min - left_max > max_distance:
max_distance = buckets[i].min - left_max
left_max = buckets[i].max
return max_distance
my_array = list([2, 6, 3, 4, 5, 10, 9])
print(get_max_sorted_distance(my_array))
代码的前几步都比较直观,唯独第四步稍微有些不好理解:使用临时变量 left_max,在每一轮迭代时存储当前左侧桶的最大值。而两个桶之间的差值,则是 buckets[i].min- left_max。
用栈实现队列
题目
用栈来模拟一个队列,要求实现队列的两个基本操作:入队、出队。
解题思路
栈的特点是 先入后出,出入元素都是在同一端(栈顶)。队列的特点是 先入先出,出入元素是在两端(队头和队尾)。
用两个栈来模拟一个队列,可以让其中一个栈作为队列的入口,负责插入新元素;另一个栈作为队列的出口,负责移除老元素。
队列的主要操作无非有两个:入队和出队。
在模拟入队操作时,每一个新元素都被压入栈A 当中。让元素1 入队、让元素2 入队、让元素3 入队。
这时,希望最先入队的元素1 出队,让栈A 中的所有元素按顺序出栈,再按照出栈顺序压入栈B。这样一来,元素从栈A 弹出并压入栈B 的顺序是 3、2、1,和当初进入栈A 的顺序 1、2、3 是相反的。此时让元素1 出队,也就是让元素1 从栈B 中弹出。
代码
class StackQueue:
def __init__(self):
self.stackA = []
self.stackB = []
def en_queue(self, element):
self.stackA.append(element)
def de_queue(self):
if len(self.stackB) == 0:
if len(self.stackA) == 0:
raise Exception('栈已经空了!')
self.transfer()
return self.stackB.pop()
def transfer(self):
while len(self.stackA) > 0:
self.stackB.append(self.stackA.pop())
stack_queue = StackQueue()
stack_queue.en_queue(1)
stack_queue.en_queue(2)
stack_queue.en_queue(3)
print(stack_queue.de_queue())
print(stack_queue.de_queue())
stack_queue.en_queue(4)
print(stack_queue.de_queue())
print(stack_queue.de_queue())
相关信息
入队操作的时间复杂度显然是 O(1)。
至于出队操作,如果涉及栈A 和栈B 的元素迁移,那么一次出队的时间复杂度是 O(n);如果不用迁移,时间复杂度是 O(1)
这里涉及一个新的概念,叫作 均摊时间复杂度。需要元素迁移的出队操作只是少数情况,并且不可能连续出现,其后的大多数出队操作都不需要元素迁移。所以把时间均摊到每一次出队操作上面,其时间复杂度是 O(1)。这个概念并不常用,稍做了解即可
寻找全排列的下一个数
题目
给出一个正整数,找出这个正整数所有数字全排列的下一个数。就是,在一个整数所包含数字的全部组合中,找到一个大于且仅大于原数的新整数。例如:
- 如果输入
12345,则返回12354 - 如果输入
12354,则返回12435 - 如果输入
12435,则返回12453
解题思路
由固定几个数字组成的整数,在逆序排列的情况下最大,在顺序排列的情况下最小。
例如:给出 1、2、3、4、5 这几个数字。
最大的组合:54321。 最小的组合:12345。
数字的顺序和逆序,是全排列中的两种极端情况。那么普遍情况下,一个数和它最近的全排列数存在的关联如下:
例如:给出整数 12354,它包含的数字是 1、2、3、4、5,找到这些数字全排列之后仅大于原数的新整数。
为了和原数接近,需要 尽量保持高位不变,低位在最小的范围内变换顺序。至于变换顺序的范围大小,则取决于当前整数的 逆序区域。
1 2 3 5 4
╰┈┈┬┈┈╯
逆序区域
如上所示,12354 的逆序区域是 最后两位,仅看这两位已经是当前的最大组合。若想最接近原数,又比原数更大,必须从 倒数第三位 开始改变。
12354 的倒数第三位是 3,需要从后面的逆序区域中找到大于 3 的最小的数字,让其和 3 的位置进行互换。
互换后的临时结果是 12453,倒数第三位已经确定,这个时候最后两位仍然是逆序状态。需要把最后两位转变为顺序状态,以此保证在倒数第三位数值为 4 的情况下,后两位尽可能小。这样一来,就得到了想要的结果 12435。
获得全排列下一个数的三个步骤:
从后向前查看 逆序区域,找到逆序区域的前一位,也就是数字置换的边界。
让逆序区域的前一位和逆序区域中大于它的最小的数字 交换位置。
把原来的逆序区域转为顺序状态。
代码
def find_nearest_number(numbers = []):
# 1. 从后向前查看逆序区域,找到逆序区域的前一位,也就是数字置换的边界
index = find_transfer_point(numbers)
# 如果数字置换边界是 0,说明整个数组已经逆序,无法得到更大的相同数字组成的整数,返回 null
if index == 0:
return None
# 2. 让逆序区域的前一位和逆序区域中大于它的最小的数字交换位置,复制入参,避免直接修改入参
numbers_copy = numbers.copy()
exchange_head(index, numbers_copy)
# 3. 把原来的逆序区域转为顺序状态
reverse(index, numbers_copy)
return numbers_copy
def find_transfer_point(numbers = []):
for i in range(len(numbers) - 1, 0, -1):
if numbers[i] > numbers[i - 1]:
return i
return 0
def exchange_head(index, numbers = []):
head = numbers[index - 1]
for i in range(len(numbers) - 1, 0, -1):
if head < numbers[i]:
numbers[index - 1] = numbers[i]
numbers[i] = head
break
return numbers
def reverse(index, numbers = []):
i = index
j = len(numbers) - 1
while i < j:
temp = numbers[i]
numbers[i] = numbers[j]
numbers[j] = temp
i += 1
j -= 1
return numbers
def output_numbers(numbers = []):
for i in numbers:
print(i, end='')
print()
my_numbers = list([1, 2, 3, 4, 5])
# 打印 12345 之后的十个全排列整数
for k in range(0, 10):
my_numbers = find_nearest_number(my_numbers)
output_numbers(my_numbers)
这种解法拥有一个 “高大上” 的名字:字典序算法。
相关信息
该算法三个步骤每一步的时间复杂度都是 O(n),所以整体时间复杂度也是 O(n)
删去 k 个数字后的最小值
题目
给出一个整数,从该整数中去掉 k 个数字,要求剩下的数字形成的新整数尽可能小。应该如何选取被去掉的数字?
其中整数的长度大于或等于 k,给出的整数的大小可以超越 Python 语言中整型类型的最大值。例如:
假设给出一个整数 1593212,删去 3 个数字(5、9、3),新整数最小的情况是 1212。
假设给出一个整数 30200,删去 1 个数字(3),新整数最小的情况是 200。
假设给出一个整数 10,删去 2 个数字(1、0。注意,这里要求删去的不是 1 个数字,而是 2 个),新整数的最小情况是 0。
解题思路
例如:给出一个整数 541270936,要求删去 1 个数字,让剩下的整数尽可能小。
此时,无论删除哪一个数字,最后的结果都是从 9 位整数变成 8 位整数。既然同样是 8 位整数,显然应该优先把 高位的数字降低,这样对新整数的值影响最大。
把 原整数的所有数字从左到右进行比较,如果发现某一位数字大于它右面的数字,那么在删除该数字后,必然会使该数位的值降低,因为右面比它小的数字顶替了它的位置。
所以,对于整数 541270936,删除一个数字所能得到的最小值是 41270936。那么对于 41270936,删除一个数字后的最小值是 1270936。那么对于 1270936,删除一个数字后的最小值是 120936。
像这样依次求得局部最优解,最终得到全局最优解的思想,叫作 贪心算法。
代码
def remove_k_digits(num, k):
for i in range(0, k):
has_cut = False
# 从左向右遍历,找到比自己右侧大的数字并删除
for j in range(0, len(num) - 1):
if num[j] > num[j + 1]:
num = num[0:j] + num[j + 1: len(num)]
has_cut = True
break
# 如果没有找到要删除的数字,则删除最后一个数字
if not has_cut:
num = num[0:len(num) - 1]
# 清除整数左侧的数字 0
for j in range(0, len(num) - 1):
if num[0] != '0':
break
num = num[1:len(num)]
# 如果整数的所有数字都被删除了,直接返回 0
if len(num) == 0:
return '0'
return num
print(remove_k_digits('1593212', 3))
print(remove_k_digits('30200', 2))
print(remove_k_digits('10', 2))
print(remove_k_digits('541270936', 3))
print(remove_k_digits('1593212', 4))
代码使用了两层循环,外层循环次数就是要删除的数字个数 k,内层循环从左到右遍历所有数字。当遍历到需要删除的数字时,利用 Python 的字符串截取方法把对应的数字删除,并重新拼接字符串。
相关信息
这段代码的时间复杂度是 O(kn)
以上代码性能不太好,主要是以下两个方面:
每一次内层循环都需要从头开始遍历所有数字。
例如:给出的整数是
11111111111114132,在第一轮循环中,需要遍历大部分数字,一直遍历到数字4,发现4 > 1,从而删除4。以目前的代码逻辑,下一轮循环时,还要从头开始遍历,再次重复遍历大部分数字,一直遍历到数字
3,发现3 > 2,从而删除3。事实上,应该停留在上一次删除的位置继续进行比较,而不是再次从头开始遍历。
字符串截取方法本身性能不高。
字符串截取方法的底层实现,涉及新字符串的创建,以及逐个字符的复制。这个方法自身的时间复杂度是 O(n)。
因此,应该避免在每删除一个数字后就进行字符串的截取和拼接。
以遍历数字作为外循环,以 k 作为内循环代码:
优化代码
def remove_k_digits_v2(num, k):
# 新整数的最终长度 = 原整数长度 - k
new_length = len(num) - k
# 创建一个栈,用于接收所有的数字
stack = []
for i in range(0, len(num)):
# 遍历当前数字
c = num[i]
# 当栈顶数字大于遍历到的当前数字时,栈顶数字出栈(相当于删除数字)
while (len(stack) > 0) and (stack[len(stack) - 1] > c) and (k > 0):
stack.pop()
k -= 1
# 如果遇到数字 0,且栈为空,0 不入栈
if ('0' == c) and (len(stack) == 0):
new_length -= 1
if new_length <= 0:
return '0'
continue
# 遍历到的当前数字入栈
stack.append(c)
# 找到栈中第一个非零数字的位置,以此构建新的整数字符串
if new_length <= 0:
return '0'
return ''.join(stack)
print(remove_k_digits_v2('1593212', 3))
print(remove_k_digits_v2('30200', 2))
print(remove_k_digits_v2('10', 2))
print(remove_k_digits_v2('541270936', 3))
print(remove_k_digits_v2('1593212', 4))
上述代码非常巧妙地运用了栈的特性,在遍历原整数的数字时,让所有数字一个一个入栈,当某个数字需要被删除时,让该数字出栈。最后,程序把栈中的元素转化为字符串类型的结果。
下面仍然以整数 541270936,k = 3 为例。当遍历到数字 5 时,数字 5 入栈。
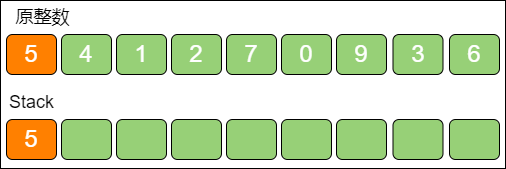
当遍历到数字 4 时,发现栈顶 5 > 4,栈顶5 出栈,数字 4 入栈。
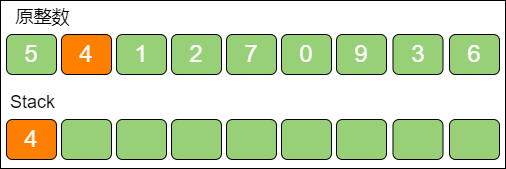
当遍历到数字 1 时,发现栈顶 4 > 1,栈顶4 出栈,数字 1 入栈。
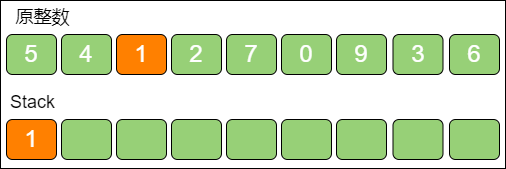
继续遍历数字 2、数字 7,并依次入栈。
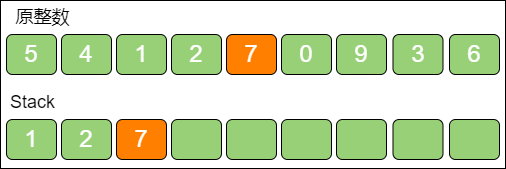
最后,遍历数字 0,发现栈顶 7 > 0,栈顶7 出栈,数字 0 入栈。
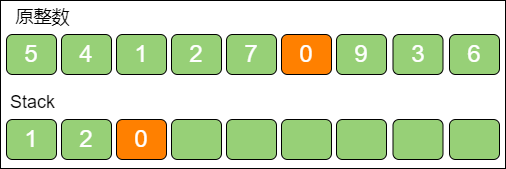
此时 k 的次数已经用完,无须再比较,让剩下的数字一起入栈即可。
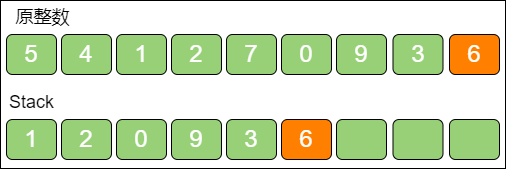
此时栈中的元素就是最终的结果。
相关信息
上面的方法只对所有数字遍历了一次,遍历的时间复杂度是 O(n),把栈转化为字符串的时间复杂度也是 O(n),所以最终的时间复杂度是 O(n)
同时,程序中利用栈来回溯遍历过的数字及删除数字,所以程序的空间复杂度是 O(n)
找到两个数组的中位数
题目
给定两个升序数组,如何找出这两个数组归并以后新的升序数组的中位数。例如:
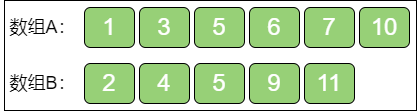
上图这两个给定数组A 和数组B,一个长度是 6,一个长度是 5,归并之后的大数组仍然要保持升序,结果如下:

大数组的长度是奇数(11),中位数显然是位于正中的第六个元素,也就是元素5。
上面的例子是奇数个元素的情况。那么如果是偶数个元素。例子:
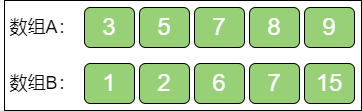
上图这两个给定数组A 和数组B,长度都是 5,归并之后的大数组如下:

大数组的长度是偶数(10),位于正中的元素有两个,分别是 6 和 7,这时候的中位数就是两个数的平均值,也就是 6.5。
解题思路
方法1:
直接把两个数组进行归并操作,中位数结果就出来。
相关信息
如果两个数组长度分别是 m 和 n,这样做的时间复杂度和空间复杂度都是 O(m + n)
方法2:
中位数把一个升序数组分成了长度相等的两部分,其中左半部分的最大值永远小于或等于右半部分的最小值。
- 对于偶数长度的数组,例如:
1, 2, 3, 5, 6, 7, 7, 8, 9, 15。可以根据中位数分成长度相等的两部分,左半部分的最大元素(6),永远小于或等于右半部分的最小元素(7) - 对于奇数长度的数组,例如:
1, 2, 3, 4, 5, 5, 6, 8, 9, 10, 11。如果把中位数本身归入左半部分,则 左半边长度 = 右半边长度 + 1。左半部分的最大元素(5),永远小于或等于右半部分的最小元素(6)
大数组的左右两部分,分别来源于两个初始数组A 和数组B 的左右部分。
大数组被中位数等分的左右两部分,每一部分根据来源又可以再划分成两部分,其中一部分来自数组A 的元素,另一部分来自数组B 的元素:
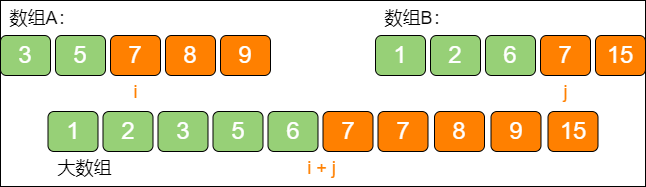
如上图所示,原始数组A 和数组B,各自分成绿色和橙色两部分。其中数值较小的绿色元素组成了大数组的左半部分,数值较大的橙色元素组成了大数组的右半部分。
最重要的是,绿色元素和橙色元素的数量是相等的(偶数情况),而且最大的绿色元素小于或等于最小的橙色元素。
假设数组A 的长度是 m,绿色和橙色元素的分界点是 i,数组B 的长度是 n,绿色和橙色元素的分界点是 j,那么为了让大数组的左右两部分长度相等,则 i 和 j 需要符合如下两个条件:
i + j = (m + n + 1) / 2(之所以 m + n 后面要再加 1,是为了应对大数组长度为奇数的情况)。
Max(A[i - 1], B[j - 1]) <= Min(A[i], B[j])(直白地说,就是最大的绿色元素小于或等于最小的橙色元素)。
由于 m + n 的值是恒定的,所以只要确定一个合适的 i,就可以确定 j,从而找到大数组左半部分和右半部分的分界,也就找到了归并之后大数组的中位数。
利用 二分查找 来确定 i 值。例如:
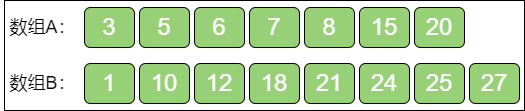
第一步,就像二分查找那样,把 i 设在数组A 的正中位置,也就是让 i = 3:
第二步,根据 i 的值来确定 j 的值,j = (m + n + 1) / 2 - i = 5:
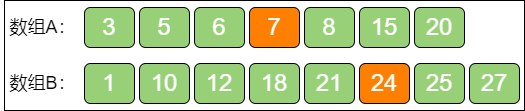
第三步,验证 i 和 j,分为下面三种情况:
B[j - 1] ≤ A[i] && A[i - 1] ≤ B[j]说明
i和j左侧的元素都小于或等于右侧的元素,这一组i和j是合适的。A[i] < B[j - 1]说明
i对应的元素偏小了,i应该向右侧移动。A[i - 1] > B[j]说明
i - 1对应的元素偏大了,i应该向左侧移动。
显然,图中的例子属于情况 2,A[3] < B[5],所以 i 应该向右移动。
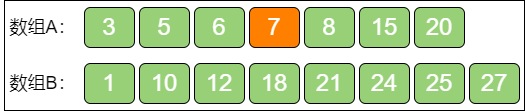
第四步,在数组A 的右半部分,重新确定 i 的位置,就像二分查找一样:
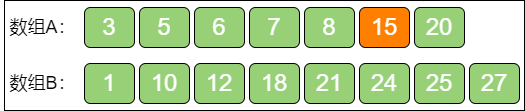
第五步,同第二步,根据 i 的值来确定 j 的值,j = (m + n + 1) / 2 - i = 3:
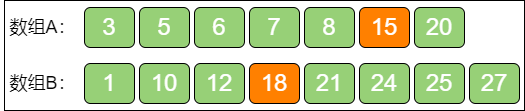
第六步,同第三步,验证 i 和 j:
由于 A[5] >= B[2] 且 B[3] >= A[4],所以这一组 i 和 j 是合适的。
第七步,找出中位数:
如果大数组的长度是奇数,那么:中位数 = Max(A[i - 1], B[j - 1])(也就是大数组左半部分的最大值)。
如果大数组的长度是偶数,那么:中位数 = (Max(A[i - 1], B[j - 1]) + Min(A[i], B[i])) / 2(也就是大数组左半部分的最大值和大数组右半部分的最小值取平均)。
在本例中,大数组的长度是奇数,所以 中位数 = Max(8, 12) = 12。
不过有些特殊情况,比如:数组A 的长度远大于数组B 的长度,或者在数组A 中无法找到合适的 i 值……处理方法如下:
数组A 的长度远大于数组B。
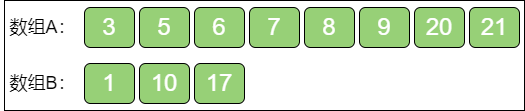
find_median_array_10 也就是
m远大于n时,当设定了i的初值,也就是数组A 正中间的元素,再计算j的时候有可能发生数组越界。因此,可以提前把数组A 和数组B 进行交换,较短的数组放在前面,
i从较短的数组中取。这样做还有一个好处,由于数组A 是较短数组,i的搜索次数减少了。无法找到合适的
i值。有两种情况:
数组A 的长度小于数组B 的长度,并且数组A 的所有元素都大于数组B 的元素
find_median_array_11 在这种情况下,无法通过二分查找寻找到符合
B[j - 1] ≤ A[i] && A[i - 1] ≤ B[j]的i值,一直到i = 0为止。此时可以跳出二分查找的循环,所求的中位数是
B[j - 1](仅限奇数情况)。数组A 的长度小于数组B 的长度,并且数组A 的所有元素都小于数组B 的元素
find_median_array_12 在这种情况下,同样无法通过二分查找寻找到符合
B[j - 1] ≤ A[i] && A[i - 1] ≤ B[j]的i值,一直到i = (数组A 的长度 - 1)为止。此时可以跳出二分查找的循环,所求的中位数是
Max(A[i - 1], B[j - 1])(仅限奇数情况)。
代码
def find_median_sorted_arrays(array_A, array_B):
m, n = len(array_A), len(array_B)
# 如果数组A 的长度大于等于数组B 的长度,则交换数组
if m > n:
array_A, array_B, m, n = array_B, array_A, n, m
if n == 0:
raise ValueError
start, end, half_len = 0, m, (m + n + 1) // 2
while start <= end:
i = (start + end) // 2
j = half_len - i
if (i < m) and (array_B[j - 1] > array_A[i]):
# i 偏小了,需要右移
start = i + 1
elif (i > 0) and (array_A[i - 1] > array_B[j]):
# i 偏大了,需要左移
end = i - 1
else:
# i 刚好合适,或 i 已达到数组边界
if i == 0:
max_of_left = array_B[j - 1]
elif j == 0:
max_of_left = array_A[i - 1]
else:
max_of_left = max(array_A[i - 1], array_B[j - 1])
if (m + n) % 2 == 1:
# 如果大数组的长度是奇数,中位数就是左半部分的最大值
return max_of_left
if i == m:
min_of_right = array_B[j]
elif j == n:
min_of_right = array_A[i]
else:
min_of_right = min(array_A[i], array_B[j])
# 如果大数组的长度是偶数,取左侧最大值和右侧最小值的平均
return (max_of_left + min_of_right) / 2.0
my_array_A = list([3, 5, 6, 7, 8, 12, 20])
my_array_B = list([1, 10, 17, 18])
print(find_median_sorted_arrays(my_array_A, my_array_B))
相关信息
由于最初的交换,数组A 的长度是 m、n 中的较小值,而确定 i 的过程类似二分查找,所以时间复杂度是 O(log2min(m, n))
如何求解金矿问题
题目
很久很久以前,有一位国王拥有 5 座金矿,每座金矿的黄金储量不同,需要参与挖掘的工人人数也不同。例如:
- 金矿储量是
200kg黄金,需要3个工人来挖掘 - 金矿储量是
300kg黄金,需要4个工人来挖掘 - 金矿储量是
350kg黄金,需要3个工人来挖掘 - 金矿储量是
400kg黄金,需要5个工人来挖掘 - 金矿储量是
500kg黄金,需要5个工人来挖掘
如果参与挖矿的工人的总数是 10。每座金矿要么全挖,要么不挖,不能派出一半人挖取一半的金矿。要求用程序求出,要想得到尽可能多的黄金,应该选择挖取哪几座金矿?
解题思路
方法1:
可以按照金矿的性价比从高到低进行排序,优先选择性价比最高的金矿来挖掘,然后是性价比第二的……
金矿按照性价比从高到低进行排序,排名结果如下:
- 第一名,350kg黄金/3人的金矿,人均产量约为
116.6kg黄金 - 第二名,500kg黄金/5人的金矿,人均产量为
100kg黄金 - 第三名,400kg黄金/5人的金矿,人均产量为
80kg黄金 - 第四名,300kg黄金/4人的金矿,人均产量为
75kg黄金 - 第五名,200kg黄金/3人的金矿,人均产量约为
66.6kg黄金
由于工人数量是 10 人,按优先挖掘性价比排名为第一名和第二名的金矿之后,工人还剩下 2 人,不够再挖掘其他金矿了。
所以,得出的最佳金矿收益是 350 + 500 即 850kg 黄金。使用 贪心算法 在局部情况下是最优解,但是在整体上却未必是最优的。
方法2:
使用 动态规划 方法,就是将复杂的问题简化成规模较小的子问题,再从简单的子问题自底向上一步一步递推,最终得到复杂问题的最优解。
首先,对于问题中的金矿来说,每一个金矿都存在着 “挖” 和 “不挖” 两种选择。假设一下,如果最后一个金矿注定不被挖掘,那么问题将简化成了 10 个工人在前 4 个金矿中做出最优选择。
10 人 5 金矿的最优选择:
- 400kg黄金/5人的金矿;500kg黄金/5人的金矿
- 200kg黄金/3人的金矿;300kg黄金/4人的金矿;350kg黄金/3人的金矿
10 人 4 金矿的最优选择:
- 400kg黄金/5人的金矿;500kg黄金/5人的金矿
- 200kg黄金/3人的金矿;300kg黄金/4人的金矿;
350kg黄金/3人的金矿
相应地,假设最后一个金矿一定会被挖掘,那么问题将简化成了 7 个工人在前 4 个金矿中做出最优选择。
10 人 5 金矿的最优选择:
- 400kg黄金/5人的金矿;500kg黄金/5人的金矿
- 200kg黄金/3人的金矿;300kg黄金/4人的金矿;350kg黄金/3人的金矿
7 人 4 金矿的最优选择:
- 400kg黄金/5人的金矿;500kg黄金/5人的金矿 + 350kg黄金/3人的金矿
- 200kg黄金/3人的金矿;300kg黄金/4人的金矿 + 350kg黄金/3人的金矿
这两种简化情况,被称为全局问题的两个 最优子结构。
最后一个金矿到底该不该挖,那就要看 10 个工人在前 4 个金矿的收益,和 7 个工人在前 4 个金矿的收益加最后一个金矿的收益谁大谁小了。
同样的道理,对于前 4 个金矿的选择,还可以做进一步简化。
首先针对 10 个工人 4 个金矿这个子结构,第 4 个金矿(300kg黄金/4人)可以选择挖与不挖。根据第 4 个金矿的选择,问题又简化成了两种更小的子结构:
10个工人在前3个金矿中做出最优选择。6(10 - 4 = 6)个工人在前3个金矿中做出最优选择。
相应地,对于 7 个工人 4 个金矿这个子结构,第 4 个金矿同样可以选择挖与不挖。根据第 4 个金矿的选择,问题也简化成了两种更小的子结构:
7个工人在前3个金矿中做出最优选择。3(7 - 4 = 3)个工人在前3个金矿中做出最优选择。 ……
就这样,问题一分为二,二分为四,一直把问题简化成在 0 个金矿或 0 个工人时的最优选择,这个收益结果显然是 0,也就是问题的 边界。
这就是动态规划的要点:确定全局最优解和最优子结构之间的关系,以及问题的边界。
这个关系用数学公式来表达的话,叫作 状态转移方程式。
把金矿数量设为 n,工人数量设为 w,金矿的含金量设为数组 g[],金矿所需开采人数设为数组 p[],设 F(n, w) 为 n 个金矿、w 个工人时的最优收益函数,那么状态转移方程式如下:
F(n, w) = 0(n = 0 或 w = 0)
问题边界,金矿数为 0 或工人数为 0 的情况:
F(n, w) = F(n - 1, w)(n ≥ 1, w < p[n - 1])
当所剩工人不够挖掘当前金矿时,只有一种最优子结构:
F(n, w)= max(F(n - 1, w), F(n - 1, w - p[n - 1]) + g[n - 1])(n ≥ 1, w ≥ p[n - 1])
在常规情况下,具有两种最优子结构(挖当前金矿或不挖当前金矿)。
递归方式代码
def get_best_gold_mining(w, n, p = [], g = []):
"""
:param w:工人数量
:param n:可选金矿数量
:param p:金矿开采所需工人数量
:param g:金矿储量
:return:最优收益
"""
if (w == 0) or (n == 0):
return 0
if w < p[n - 1]:
return get_best_gold_mining(w, n - 1, p, g)
return max(get_best_gold_mining(w, n - 1, p, g),
get_best_gold_mining(w - p[n - 1], n - 1, p, g) + g[n - 1])
print(get_best_gold_mining(10, 5, p = [5, 5, 3, 4, 3], g = [400, 500, 200, 300, 350]))
全局问题经过简化,会拆解成两个子结构;两个子结构再次简化,会拆解成 4 个更小的子结构……如果金矿数量是 n,工人数量充足,时间复杂度就是 O(2n)。
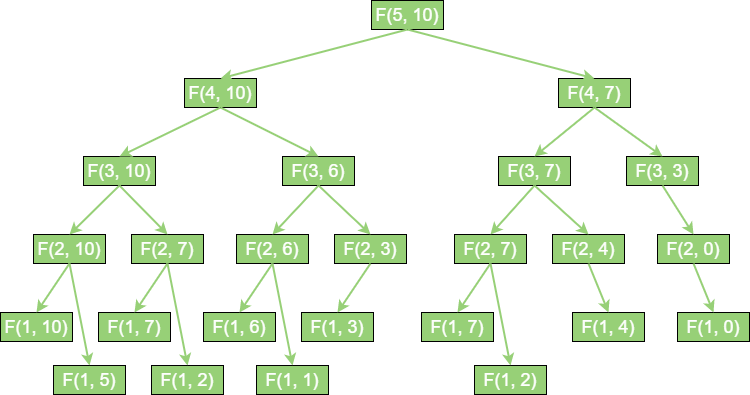
如果只有 5 个金矿,问题还不算严重。如果金矿数量有 50 个,甚至 100 个,这样的时间复杂度是根本无法接受的。递归之所以低效的根本原因,那就是因为递归做了许多重复的计算。如下所示:
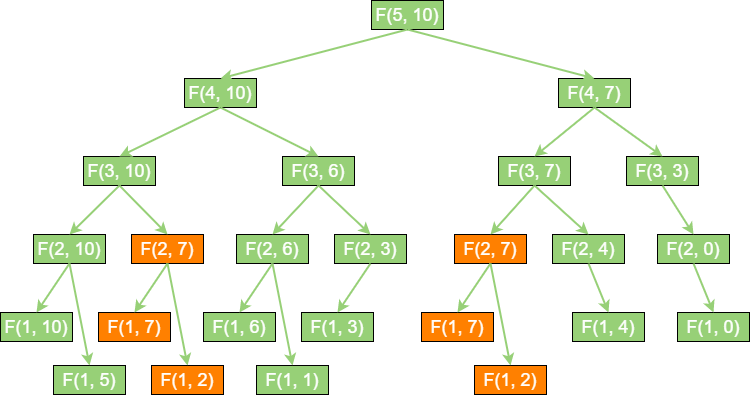
在上图中,标为橘色的方法调用是重复的。可以看到 F(2, 7)、F(1, 7)、F(1, 2) 这几个入参相同的方法都被调用了两次。
当金矿数量为 5 时,重复调用的问题还不太明显。金矿数量越多,递归层次越深,重复调用也就越多,这些无谓的调用必然会降低程序的性能。
为了避免这些重复调用,就用到动态规划的另一个核心要点:自底向上求解。例如:
在进行求解之前,先准备一张表格,用于记录选择金矿的中间数据。
| 1 个工人 | 2 个工人 | 3 个工人 | 4 个工人 | 5 个工人 | 6 个工人 | 7 个工人 | 8 个工人 | 9 个工人 | 10 个工人 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 400kg黄金/5人 | ||||||||||
| 500kg黄金/5人 | ||||||||||
| 200kg黄金/3人 | ||||||||||
| 300kg黄金/4人 | ||||||||||
| 350kg黄金/3人 |
表格最左侧代表不同的金矿选择范围,从上到下,每多增加 1 行,可就代表多 1 个金矿供选择,也就是 F(n, w) 函数中的 n 值。表格的最上方代表工人数量,从 1 个工人到 10 个工人,也就是 F(n, w) 函数中的 w 值。其余空白的格子,都是等待填写的,代表当给出 n 个金矿、w 个工人时的最优收益,也就是 F(n, w) 的值。
下面从第 1 行第 1 列开始,尝试把空白的格子一一填满,填充的依据就是 状态转移方程式。
对于第 1 行的前 4 个格子,由于 w < p[n - 1],对应的状态转移方程式如下:
F(n, w) = F(n - 1, w)(n > 1, w < p[n - 1])
带入求解:
F(1, 1) = F(1 - 1, 1) = F(0, 1) = 0
F(1, 2) = F(1 - 1, 2) = F(0, 2) = 0
F(1, 3) = F(1 - 1, 3) = F(0, 3) = 0
F(1, 4) = F(1 - 1, 4) = F(0, 4) = 0
| 1 个工人 | 2 个工人 | 3 个工人 | 4 个工人 | 5 个工人 | 6 个工人 | 7 个工人 | 8 个工人 | 9 个工人 | 10 个工人 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 400kg黄金/5人 | 0 | 0 | 0 | 0 | ||||||
| 500kg黄金/5人 | ||||||||||
| 200kg黄金/3人 | ||||||||||
| 300kg黄金/4人 | ||||||||||
| 350kg黄金/3人 |
第 1 行的后 6 个格子计算,此时 w ≥ p[n - 1],对应的状态转移方程式如下:
F(n, w) = max(F(n - 1, w), F(n - 1, w - p[n - 1]) + g[n - 1])(n > 1, w ≥ p[n - 1])
带入求解:
F(1, 5) = max(F(1 - 1, 5), F(1 - 1, 5 - 5) + 400) = max(F(0, 5), F(0, 0) + 400) = max(0, 400) = 400
F(1, 6) = max(F(1 - 1, 6), F(1 - 1, 6 - 5) + 400) = max(F(0, 6), F(0, 1) + 400) = max(0, 400) = 400
……
F(1, 10) = max(F(1 - 1, 10), F(1 - 1, 10 - 5) + 400) = max(F(0, 10), F(0, 5) + 400) = max(0, 400) = 400
| 1 个工人 | 2 个工人 | 3 个工人 | 4 个工人 | 5 个工人 | 6 个工人 | 7 个工人 | 8 个工人 | 9 个工人 | 10 个工人 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 400kg黄金/5人 | 0 | 0 | 0 | 0 | 400 | 400 | 400 | 400 | 400 | 400 |
| 500kg黄金/5人 | ||||||||||
| 200kg黄金/3人 | ||||||||||
| 300kg黄金/4人 | ||||||||||
| 350kg黄金/3人 |
对于第 2 行的前 4 个格子,和第 1 行同理,由于 w < p[n - 1],对应的状态转移方程式如下:
F(n, w) = F(n - 1, w)(n > 1, w < p[n - 1])
带入求解:
F(2, 1) = F(2 - 1, 1) = F(1, 1) = 0
F(2, 2) = F(2 - 1, 2) = F(1, 2) = 0
F(2, 3) = F(2 - 1, 3) = F(1, 3) = 0
F(2, 4) = F(2 - 1, 4) = F(1, 4) = 0
| 1 个工人 | 2 个工人 | 3 个工人 | 4 个工人 | 5 个工人 | 6 个工人 | 7 个工人 | 8 个工人 | 9 个工人 | 10 个工人 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 400kg黄金/5人 | 0 | 0 | 0 | 0 | 400 | 400 | 400 | 400 | 400 | 400 |
| 500kg黄金/5人 | 0 | 0 | 0 | 0 | ||||||
| 200kg黄金/3人 | ||||||||||
| 300kg黄金/4人 | ||||||||||
| 350kg黄金/3人 |
第 2 行的后 6 个格子,和第 1 行同理,此时 w ≥ p[n - 1],对应的状态转移方程式如下:
F(n, w) = max(F(n - 1, w), F(n - 1, w - p[n - 1]) + g[n - 1])(n > 1, w ≥ p[n - 1])
带入求解:
F(2, 5) = max(F(2 - 1, 5), F(2 - 1, 5 - 5) + 500) = max(F(1, 5), F(1, 0) + 500) = max(400, 500) = 500
F(2, 6) = max(F(2 - 1, 6), F(2 - 1, 6 - 5) + 500) = max(F(1, 6), F(1, 1) + 500) = max(400, 500) = 500
……
F(2, 10) = max(F(2 - 1, 10), F(2 - 1, 10 - 5) + 500) = max(F(1, 10), F(1, 5) + 500) = max(400, 400 + 500) = 900
| 1 个工人 | 2 个工人 | 3 个工人 | 4 个工人 | 5 个工人 | 6 个工人 | 7 个工人 | 8 个工人 | 9 个工人 | 10 个工人 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 400kg黄金/5人 | 0 | 0 | 0 | 0 | 400 | 400 | 400 | 400 | 400 | 400 |
| 500kg黄金/5人 | 0 | 0 | 0 | 0 | 500 | 500 | 500 | 500 | 500 | 900 |
| 200kg黄金/3人 | ||||||||||
| 300kg黄金/4人 | ||||||||||
| 350kg黄金/3人 |
同理可得出之后的答案:
| 1 个工人 | 2 个工人 | 3 个工人 | 4 个工人 | 5 个工人 | 6 个工人 | 7 个工人 | 8 个工人 | 9 个工人 | 10 个工人 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 400kg黄金/5人 | 0 | 0 | 0 | 0 | 400 | 400 | 400 | 400 | 400 | 400 |
| 500kg黄金/5人 | 0 | 0 | 0 | 0 | 500 | 500 | 500 | 500 | 500 | 900 |
| 200kg黄金/3人 | 0 | 0 | 200 | 200 | 500 | 500 | 500 | 700 | 700 | 900 |
| 300kg黄金/4人 | 0 | 0 | 200 | 300 | 500 | 500 | 500 | 700 | 800 | 900 |
| 350kg黄金/3人 | 0 | 0 | 350 | 350 | 500 | 550 | 650 | 850 | 850 | 900 |
此时,最后 1 行最后 1 个格子所填的 900 就是最终要求的结果,即 5 个金矿、10 个工人的最优收益是 900kg 黄金。
二维数组方式代码
def get_best_gold_mining_v2(w, p = [], g = []):
"""
:param w:工人数量
:param p:金矿开采所需工人数量
:param g:金矿储量
:return:最优收益
"""
result_table = [[0 for i in range(w + 1)] for i in range(len(g) + 1)]
# 填充表格
for i in range(1, len(g) + 1):
for j in range(1, w + 1):
if j < p[i - 1]:
result_table[i][j] = result_table[i - 1][j]
else:
result_table[i][j] = max(result_table[i - 1][j], result_table[i - 1][j - p[i - 1]] + g[i - 1])
# 返回最后一个格子的值
return result_table[len(g)][w]
print(get_best_gold_mining_v2(10, p = [5, 5, 3, 4, 3], g = [400, 500, 200, 300, 350]))
相关信息
程序利用双循环来填充一个二维数组,所以时间复杂度和空间复杂度都是 O(nw)
上述代码在时间上已经没有什么可优化的了,但是在空间上还可以做一些优化。在表格中除第 1 行之外,每一行的结果都是由上一行数据推导出来的。以 4 个金矿 9 个工人为例:
4 个金矿、9 个工人的最优结果,是由它的两个最优子结构,也就是 3 个金矿、5 个工人和 3 个金矿、9 个工人的结果推导而来的。这两个最优子结构都位于它的上一行。所以,在程序中并不需要保存整个表格,无论金矿有多少座,只保存 1 行的数据即可。在计算下一行时,要 从右向左 统计,把旧的数据一个一个替换掉。
二维数组方式代码优化
def get_best_gold_mining_v3(w, p = [], g = []):
"""
:param w:工人数量
:param p:金矿开采所需工人数量
:param g:金矿储量
:return:最优收益
"""
result = [0] * (w + 1)
# 填充一维数组
for i in range(1, len(g) + 1):
for j in range(w, 0, -1):
if j >= p[i - 1]:
result[j] = max(result[j], result[j - p[i - 1]] + g[i - 1])
# 返回最后一个格子的值
return result[w]
print(get_best_gold_mining_v3(10, p = [5, 5, 3, 4, 3], g = [400, 500, 200, 300, 350]))
相关信息
优化后的空间复杂度降低到了 O(n)
从右向左统计原因
在计算 result[j - p[i - 1]] + g[i - 1] 值时,要获取上一行的旧数据(比当前下标小),如果从左往右统计,当前位置左侧的数据已经全是本行的新数据,获取不到上一行的旧数据导致结果错误
寻找缺失的整数
题目
在一个无序数组里有 99 个不重复的正整数,范围是 1~100,唯独缺少 1 个 1~100 中的整数。如何找出这个缺失的整数?
解题思路
方法1:
创建一个哈希表,以 1~100 这 100 个整数为 Key。然后遍历整个数组,每读到一个整数,就定位到哈希表中对应的 Key,然后删除这个 Key。
由于数组中缺少 1 个整数,哈希表最终一定会有 99 个 Key 被删除,从而剩下 1 个 Key。这个剩下的 Key 就是那个缺失的整数。
相关信息
假设数组长度是 n,那么该解法的时间复杂度是 O(n),空间复杂度是 O(n)
方法2:
先把数组元素从小到大进行排序,然后遍历已经有序的数组,如果发现某两个相邻元素并不连续,说明缺少的就是这两个元素之间的整数。
相关信息
假设数组长度是 n,如果用时间复杂度为 O(nlog2n) 的排序算法进行排序,那么该解法的时间复杂度是 O(nlog2n),空间复杂度是 O(1)
方法3:
先算出 1 + 2 + 3 + … + 100 的和,然后依次减去数组里的元素,最后得到的差值,就是那个缺失的整数。
相关信息
假设数组长度是 n,那么该解法的时间复杂度是 O(n),空间复杂度是 O(1)
问题扩展
扩展问题1:一个无序数组里有若干个正整数,范围是 1~100,其中 99 个整数都出现了偶数次,只有 1 个整数出现了奇数次,如何找到这个出现奇数次的整数?
遍历整个数组,依次做 异或运算。由于异或运算在进行位运算时,相同为 0,不同为 1,因此所有出现偶数次的整数都会相互抵消变成 0,只有唯一出现奇数次的整数会被留下。例如:给出一个无序数组 {3, 1, 3, 2, 4, 1, 4}。
异或运算像加法运算一样,满足交换律和结合律,所以这个数组元素的异或运算的结果为:
3 xor 1 xor 3 xor 2 xor 4 xor 1 xor 4
= 1 xor 1 xor 3 xor 3 xor 4 xor 4 xor 2
= 2
相关信息
假设数组长度是 n,那么该解法的时间复杂度是 O(n),空间复杂度是 O(1)
扩展问题2:假设一个无序数组里有若干个正整数,范围是 1~100,其中有 98 个整数出现了偶数次,只有 2 个整数出现了奇数次,如何找到这 2 个出现奇数次的整数?
通过 分治法 把 2 个出现了奇数次的整数命名为 A 和 B。遍历整个数组,然后依次做异或运算,进行异或运算的最终结果,等同于 A 和 B 进行异或运算的结果。在这个结果中,至少会有一个二进制位是 1(如果都是 0,说明 A 和 B 相等,和题目不相符)。
例如:给出一个无序数组 {4, 1, 2, 2, 5, 1, 4, 3},所有元素进行异或运算的结果是为:
4 xor 1 xor 2 xor 2 xor 5 xor 1 xor 4 xor 3
= 1 xor 1 xor 2 xor 2 xor 4 xor 4 xor 3 xor 5
= 3 xor 5
= 00000110B
选定该结果中值为 1 的某一位数字,如 00000110B 的倒数第 2 位是 1,这说明 A 和 B 对应的二进制的倒数第二位是不同的。其中必定有一个整数的倒数第二位是 0,另一个整数的倒数第二位是 1。
根据这个结论,可以把原数组按照二进制位的倒数第二位的不同,分成两部分,一部分的倒数第二位是 0,另一部分的倒数第二位是 1。由于 A 和 B 的倒数第二位不同,所以 A 被分配到其中一部分,B 被分配到另一部分,绝不会出现 A 和 B 在同一部分,另一部分既没有 A,也没有 B 的情况。
无序数组 {4, 1, 2, 2, 5, 1, 4, 3} 分为 {4, 1, 5, 1, 4} 到数第二位为 0 和 {2, 2, 3} 到数第二位为 1 的两组数组。按照原先的异或算法,从每一部分中找出唯一的奇数次整数即可。
相关信息
假设数组长度是 n,那么该解法的时间复杂度是 O(n)。把数组分成两部分,并不需要借助额外的存储空间,完全可以在按二进制位分组的同时来做异或运算,所以空间复杂度仍然是 O(1)
代码
def find_lost_num(array = []):
# 用于存储两个出现奇数次的整数
result = [0, 0]
# 第一次整体异或
xor_result = 0
for i in range(0, len(array)):
xor_result ^= array[i]
# 如果异或结果为 0,说明输入数组不符合要求
if xor_result == 0:
raise ValueError
# 确定两个整数的不同位,以此来做分组
separator = 1
while 0 == (xor_result & separator):
separator <<= 1
# 第二次分组异或
for i in range(0, len(array)):
if 0 == (array[i] & separator):
result[0] ^= array[i]
else:
result[1] ^= array[i]
return result
my_array = list([4, 1, 2, 2, 5, 1, 4, 3])
print(find_lost_num(my_array))
